|
Tamaño: 231
Comentario:
|
Tamaño: 1861
Comentario:
|
| Los textos eliminados se marcan así. | Los textos añadidos se marcan así. |
| Línea 6: | Línea 6: |
| == Modelo Balancín == === Continuo === |
== Modelo Balancín con Compensador PID == === Modelo Continuo === {{attachment:planta_lc_continuo.png}} $$$ \sum{\tau_x} = \tau_2 - \tau_1 = J\frac{d^2\theta}{dt^2} $$ $$$ s^2\theta_{(s)}= \frac{\tau_{(s)}}{J} $$ $$$ G_{bal(s)} = \frac{1}{Js^2} $$ $$$ G_{torque(s)} = k_\tau $$ $$$ G_{PID(s)} = k_p\cdot(1 + \frac{1}{T_is} + T_ds}) $$ $$$ G_{LA(s)} = G_{bal(s)}G_{torque(s)}G_{PID(s)} = \frac{k_pk_\tau}{T_iJ}\frac{T_iT_ds^2 + T_is + 1}{s^3} $$ $$$ G_{LC(s)} = \frac{G_{LA(s)}}{1+G_{LA(s)}} = k_pk_\tau\frac{T_iT_ds^2 + T_is + 1}{T_iJs^3 + k_pk_\tauT_iT_ds^2 + k_pk_\tauT_is + k_pk_\tau}$$ ==== Archivos para Simulaciones ==== {{attachment:PID_LA_continuo.m}} === Modelo Discreto === {{attachment:planta_lc_discreto.png}} $$$ G_{bal(s)} = \frac{1}{Js^2} $$ $$$ G_{ROC(s)}=\frac{1-e^{-TS}}{S}$$ $$$ G_{torque(s)} = k_\tau $$ $$$ G_{PID(s)} = k_p\cdot(1 + \frac{1}{T_is} + T_ds}) $$ $$$ G_{planta(Z)} = Z[G_{ROC(s)}G_{bal(s)}G_{torque(s)}] = Z[\frac{1 - e^{-TS}}{S}\frac{k_\tau}{JS^2}] = (1-z^-1)Z[\frac{2k_\tau}{2JS^3}] = \frac{T^2k_\tau}{2J}\frac{z+1}{z^2-2z+1}$$ $$$ G_{PID(Z)} = K_P + \frac{K_I}{1-z^-1} + K_D(1-z^-1) = \frac{(K_P + K_I + K_D)z^2 + ( -2K_D - K_P )z + K_D }{ z^2 - z } $$ $$$ G_{LA(Z)} = G_{PID(Z)}G_{planta(Z)} = \frac{T^2k_\tau}{2J}\frac{(K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D}{z^4-3z^3+3z^2-z} $$ $$$ G_{LC(Z)} = \frac{G_{LA(Z)}}{1+G_{LA(Z)}} = \frac{k_{\tau}T^2((K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D)}{ 2Jz^4 + ((K_P + K_I + K_D)k_{\tau}T^2 -6 )z^3 + ((K_I - K_D)k_{\tau}T^2 +6 )z^2 + ( ( -K_P - K_D ) k_{\tau} T^2 -2 )z + K_D k_{\tau} T^2 } $$ |
Tabla de Contenidos
Modelo Balancín con Compensador PID
Modelo Continuo
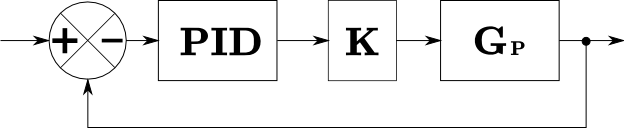
Archivos para Simulaciones
1 J = 0.0086556;
2 Kp = 1;
3 Kt = 90.63e-6;
4 Ti = 0;
5 Td = 0;
6
7 desicion = 1;
8
9 while( desicion == 1)
10
11 %Kp = input('Ingrese Kp : ');
12 Ti = input('Ingrese Ti : ');
13 Td = input('Ingrese Td : ');
14
15 num = Kp*Kt/(Ti*J)*[Ti*Td, Ti, 1];
16 den = [1, 0, 0, 0];
17
18 sistema = tf(num,den);
19
20 K_inc = input('Ingrese el incremento de K del rlocus: ');
21 K_max = input('Ingrese el K_max del rlocus: ');
22
23 %rlocus(sistema,K_inc,0,K_max);
24 rlocus(sistema);
25
26 pause;
27 desicion = input('Ingrese 1 para hacer otro rlocus: ');
28
29 end
Modelo Discreto


