Bienvenido: Ingresar
location: Diferencias para "LabElectronica/ProyectoQuadricoptero/QA3Fase1EstModYConArqRobMoviles/Balancin"
Diferencias entre las revisiones 23 y 24
⇤ ← Versión 23 con fecha 2010-10-01 23:36:36 →
Tamaño: 1768
Editor: Jaarac
Comentario:
← Versión 24 con fecha 2010-10-01 23:37:26 → ⇥
Tamaño: 1770
Editor: Jaarac
Comentario:
Los textos eliminados se marcan así. Los textos añadidos se marcan así.
Línea 43: Línea 43:
$$$ G_{LC(Z)} = \frac{G_{LA(Z)}}{1+G_{LA(Z)}} = $$ k_\tauT^2\frac{(K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D}{2Jz^4 + ((K_P + K_I + K_D)k_\tauT^2 -6 )z^3 + ((K_I - K_D)k_\tauT^2 +6 )z^2 + ((-K_P - K_D)k_\tauT^2 -2)z + K_Dk_\tauT^2} $$ $$$ G_{LC(Z)} = \frac{G_{LA(Z)}}{1+G_{LA(Z)}} = k_\tauT^2\frac{(K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D}{1}$${2Jz^4 + ((K_P + K_I + K_D)k_\tauT^2 -6 )z^3 + ((K_I - K_D)k_\tauT^2 +6 )z^2 + ((-K_P - K_D)k_\tauT^2 -2)z + K_Dk_\tauT^2} $$

Tabla de Contenidos

  1. Modelo Balancín con Compensador PID
    1. Modelo Continuo
    2. Modelo Discreto

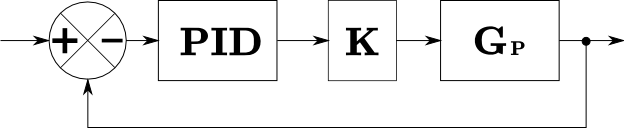
Modelo Balancín con Compensador PID

Modelo Continuo

planta_lc_continuo.png

$$$ \sum{\tau_x} = \tau_2 - \tau_1 = J\frac{d^2\theta}{dt^2} $$

$$$ s^2\theta_{(s)}= \frac{\tau_{(s)}}{J} $$

$$$ G_{bal(s)} = \frac{1}{Js^2} $$

$$$ G_{torque(s)} = k_\tau $$

$$$ G_{PID(s)} = k_p\cdot(1 + \frac{1}{T_is} + T_ds}) $$

$$$ G_{LA(s)} = G_{bal(s)}G_{torque(s)}G_{PID(s)} = \frac{k_pk_\tau}{T_iJ}\frac{T_iT_ds^2 + T_is + 1}{s^3} $$

$$$ G_{LC(s)} = \frac{G_{LA(s)}}{1+G_{LA(s)}} = k_pk_\tau\frac{T_iT_ds^2 + T_is + 1}{T_iJs^3 + k_pk_\tauT_iT_ds^2 + k_pk_\tauT_is + k_pk_\tau}$$

Modelo Discreto

planta_lc_discreto.png

$$$ G_{bal(s)} = \frac{1}{Js^2} $$

$$$ G_{ROC(s)}=\frac{1-e^{-TS}}{S}$$

$$$ G_{torque(s)} = k_\tau $$

$$$ G_{PID(s)} = k_p\cdot(1 + \frac{1}{T_is} + T_ds}) $$

$$$ G_{planta(Z)} = Z[G_{ROC(s)}G_{bal(s)}G_{torque(s)}] = Z[\frac{1 - e^{-TS}}{S}\frac{k_\tau}{JS^2}] = (1-z^-1)Z[\frac{2k_\tau}{2JS^3}] = \frac{T^2k_\tau}{2J}\frac{z+1}{z^2-2z+1}$$

$$$ G_{PID(Z)} = K_P + \frac{K_I}{1-z^-1} + K_D(1-z^-1) = \frac{(K_P + K_I + K_D)z^2 + ( -2K_D - K_P )z + K_D }{ z^2 - z } $$

$$$ G_{LA(Z)} = G_{PID(Z)}G_{planta(Z)} = \frac{T^2k_\tau}{2J}\frac{(K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D}{z^4-3z^3+3z^2-z} $$

$$$ G_{LC(Z)} = \frac{G_{LA(Z)}}{1+G_{LA(Z)}} = k_\tauT^2\frac{(K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D}{1}$$

{2Jz4 + ((K_P + K_I + K_D)k_\tauT2 -6 )z3 + ((K_I - K_D)k_\tauT2 +6 )z2 + ((-K_P - K_D)k_\tauT2 -2)z + K_Dk_\tauT^2} $$

None: LabElectronica/ProyectoQuadricoptero/QA3Fase1EstModYConArqRobMoviles/Balancin (última edición 2010-10-04 16:04:32 efectuada por Jaarac)