|
Tamaño: 8789
Comentario:
|
Tamaño: 8930
Comentario:
|
| Los textos eliminados se marcan así. | Los textos añadidos se marcan así. |
| Línea 1: | Línea 1: |
| ## page was renamed from TrabajosPracticos/PracticoADC6 ## page was renamed from PracticoADC6 |
|
| Línea 12: | Línea 14: |
| $$G = \frac{\Delta Vout}{\Delta Vin} = \frac{5}{4} = 1,25$$ | $$$G = \frac{\Delta Vout}{\Delta Vin} = \frac{5}{4} = 1,25$$ |
| Línea 21: | Línea 23: |
| $$Vo = \frac{R2}{R3}Vin +\frac{R2}{R4} VRef$$ | $$$Vo = \frac{R2}{R3}Vin +\frac{R2}{R4} VRef$$ |
| Línea 25: | Línea 27: |
| $$5 = \frac{R2}{R3}2 + \frac{R2}{R4}2$$ | $$$5 = \frac{R2}{R3}2 + \frac{R2}{R4}2$$ |
| Línea 29: | Línea 31: |
| $$5 = \frac{R2}{R3}4$$ $$\frac{R2}{R3} = \frac{5}{4}$$ |
$$$5 = \frac{R2}{R3}4$$ $$$\frac{R2}{R3} = \frac{5}{4}$$ |
| Línea 36: | Línea 38: |
| $$R1,R2 = 15K\Omega$$ $$R3,R4 = 12K\Omega$$ |
$$$R1,R2 = 15K\Omega$$ $$$R3,R4 = 12K\Omega$$ |
| Línea 46: | Línea 48: |
| $$cuentas = \frac{2}{0,5\times10^{-3}} = 4000$$ | $$$cuentas = \frac{2}{0,5\times10^{-3}} = 4000$$ |
| Línea 51: | Línea 53: |
| $$2^n = 4000$$ $$n\log{2} = \log{4000}$$ $$n=\frac{\log{4000}}{\log{2}}=11,965784285 $$ |
$$$2^n = 4000$$ $$$n\log{2} = \log{4000}$$ $$$n=\frac{\log{4000}}{\log{2}}=11,965784285 $$ |
| Línea 65: | Línea 67: |
| $$ V_{lsb}= \frac{5V}{4096} = 1,220703 mV$$ | $$$ V_{lsb}= \frac{5V}{4096} = 1,220703 mV$$ |
| Línea 69: | Línea 71: |
| $$G = \frac{V_{lsb}}{V_s} = \frac{1,220703\times10^{-3}}{0,5\times10^{-3}} = 2,441406 $$ | $$$G = \frac{V_{lsb}}{V_s} = \frac{1,220703\times10^{-3}}{0,5\times10^{-3}} = 2,441406 $$ |
| Línea 78: | Línea 80: |
| $$cuentas = \frac{3}{0,5\times10^{-3}} = 6000$$ | $$$cuentas = \frac{3}{0,5\times10^{-3}} = 6000$$ |
| Línea 83: | Línea 85: |
| $$n=\frac{\log{6000}}{\log{2}}=12,55 $$ | $$$n=\frac{\log{6000}}{\log{2}}=12,55 $$ |
| Línea 93: | Línea 95: |
| $$ V_{lsb} = \frac{5V}{8192} = 0,610352mV$$ | $$$ V_{lsb} = \frac{5V}{8192} = 0,610352mV$$ |
| Línea 96: | Línea 98: |
| $$G = \frac{V_{lsb}}{V_s} = \frac{0,610352 \times 10^{-3}}{0,5 \times 10^{-3}} = 1,2207 $$ | $$$G = \frac{V_{lsb}}{V_s} = \frac{0,610352 \times 10^{-3}}{0,5 \times 10^{-3}} = 1,2207 $$ |
| Línea 106: | Línea 108: |
| $$cuentas = \frac{2}{0,1\times10^{-3}} = 20000$$ | $$$cuentas = \frac{2}{0,1\times10^{-3}} = 20000$$ |
| Línea 111: | Línea 113: |
| $$n=\frac{\log{20000}}{\log{2}}=14,2877 $$ | $$$n=\frac{\log{20000}}{\log{2}}=14,2877 $$ |
| Línea 121: | Línea 123: |
| $$ V_{lsb} = \frac{3,5V}{32768} = 0,10681mV$$ | $$$ V_{lsb} = \frac{3,5V}{32768} = 0,10681mV$$ |
| Línea 125: | Línea 127: |
| $$G = \frac{V_{lsb}}{V_s} = \frac{0,10681\times 10^{-3} }{0,1\times 10^{-3} } = 1,07 $$ | $$$G = \frac{V_{lsb}}{V_s} = \frac{0,10681\times 10^{-3} }{0,1\times 10^{-3} } = 1,07 $$ |
| Línea 129: | Línea 131: |
| $$Vref = 0,0001V\cdot32768 = 3,28V $$ | $$$Vref = 0,0001V\cdot32768 = 3,28V $$ |
| Línea 139: | Línea 141: |
| $$paso = \frac{5000g}{2^{12}} = \frac{5000g}{4096} = 1,220703125g$$ | $$$paso = \frac{5000g}{2^{12}} = \frac{5000g}{4096} = 1,220703125g$$ |
| Línea 151: | Línea 153: |
| $$V_{lsb} = \frac{Vref}{2^n} $$ $$V_{error} = \frac{V_{lsb}}{4} = \frac{Vref}{2^n\cdot4} = \frac{5}{2^{13}\cdot4} = 0,305 mV$$ |
$$$V_{lsb} = \frac{Vref}{2^n} $$ $$$V_{error} = \frac{V_{lsb}}{4} = \frac{Vref}{2^n\cdot4} = \frac{5}{2^{13}\cdot4} = 0,305 mV$$ |
| Línea 158: | Línea 160: |
| $$E_{Vref} {{{V_{ripple} }}} \frac{V_{lsb}}{4} = 0,305 mV$$ | $$$E_{Vref} {{{V_{ripple} }}} \frac{V_{lsb}}{4} = 0,305 mV$$ |
| Línea 163: | Línea 165: |
| $$E_G =\frac{\frac{V_{lsb}}{4}}{Vref} = \frac{\frac{Vref}{2^n \cdot 4}}{Vref} = \frac{1}{2^n \cdot 4} = \frac{1}{8192\cdot4} = 30ppm$$ | $$$E_G =\frac{\frac{V_{lsb}}{4}}{Vref} = \frac{\frac{Vref}{2^n \cdot 4}}{Vref} = \frac{1}{2^n \cdot 4} = \frac{1}{8192\cdot4} = 30ppm$$ |
| Línea 168: | Línea 170: |
| $$E_G =\frac{\frac{V_{lsb}}{4}}{Vmax} = \frac{\frac{V_{lsb}}{4}}{V_{lsb}\cdot cuentas} = \frac{1}{cuentas\cdot4} = \frac{1}{6000\cdot4} = 41ppm$$ | $$$E_G =\frac{\frac{V_{lsb}}{4}}{Vmax} = \frac{\frac{V_{lsb}}{4}}{V_{lsb}\cdot cuentas} = \frac{1}{cuentas\cdot4} = \frac{1}{6000\cdot4} = 41ppm$$ |
| Línea 179: | Línea 181: |
| $$V_{error} = \frac{V_{lsb}}{4} = \frac{5}{2^{15}\cdot4} = 0,027 mV$$ | $$$V_{error} = \frac{V_{lsb}}{4} = \frac{5}{2^{15}\cdot4} = 0,027 mV$$ |
| Línea 183: | Línea 185: |
| $$V_{ripple} = \frac{V_{lsb}}{4} = 0,027 mV$$ | $$$V_{ripple} = \frac{V_{lsb}}{4} = 0,027 mV$$ |
| Línea 188: | Línea 190: |
| $$E_G = \frac{1}{32768\cdot4} = 7,6ppm$$ | $$$E_G = \frac{1}{32768\cdot4} = 7,6ppm$$ |
| Línea 193: | Línea 195: |
| $$E_G = \frac{1}{20000\cdot4} = 12ppm$$ | $$$E_G = \frac{1}{20000\cdot4} = 12ppm$$ |
| Línea 206: | Línea 208: |
| $$f_m = 5 \cdot f_{señal}$$ $$f_m = 5KHz$$ |
$$$f_m = 5 \cdot f_{señal}$$ $$$f_m = 5KHz$$ |
| Línea 213: | Línea 215: |
| $$t_c = \frac{1}{5KHz} = 200 \mu S$$ | $$$t_c = \frac{1}{5KHz} = 200 \mu S$$ |
| Línea 219: | Línea 221: |
| $$v = V \sin ( w t )$$ | $$$v = V \sin ( w t )$$ |
| Línea 223: | Línea 225: |
| $$\frac{\mathrm{d}v}{\mathrm{d}t }= V w \cos ( w t )$$ | $$$\frac{\mathrm{d}v}{\mathrm{d}t }= V w \cos ( w t )$$ |
| Línea 227: | Línea 229: |
| $$\frac{\Delta V}{ts}= V w$$ | $$$\frac{\Delta V}{ts}= V w$$ |
| Línea 231: | Línea 233: |
| $$\frac{\Delta V}{ts}= V 2 \Pi f$$ $$\Delta V = V \cdot 2 \cdot \Pi \cdot f \cdot ts$$ |
$$$\frac{\Delta V}{ts}= V 2 \Pi f$$ $$$\Delta V = V \cdot 2 \cdot \Pi \cdot f \cdot ts$$ |
| Línea 239: | Línea 241: |
| $$e = \frac{\Delta V}{2V} = \frac{V \cdot 2 \cdot \Pi \cdot f \cdot ts}{2V} = \Pi \cdot f \cdot ts$$ | $$$e = \frac{\Delta V}{2V} = \frac{V \cdot 2 \cdot \Pi \cdot f \cdot ts}{2V} = \Pi \cdot f \cdot ts$$ |
| Línea 244: | Línea 246: |
| $$e < \frac{1}{2^n \cdot 2}$$ | $$$e < \frac{1}{2^n \cdot 2}$$ |
| Línea 249: | Línea 251: |
| $$\Pi \cdot f \cdot ts < \frac{1}{2^n \cdot 2} $$ $$ts < \frac{1}{2^n \cdot 2 \cdot \Pi \cdot f} $$ |
$$$\Pi \cdot f \cdot ts < \frac{1}{2^n \cdot 2} $$ $$$ts < \frac{1}{2^n \cdot 2 \cdot \Pi \cdot f} $$ |
| Línea 255: | Línea 257: |
| $$ts =\frac{1}{2^n \cdot 2 \cdot \Pi \cdot f} = \frac{1}{2^{12} \cdot 2 \cdot \Pi \cdot 1KHz} = 39 nS $$ | $$$ts =\frac{1}{2^n \cdot 2 \cdot \Pi \cdot f} = \frac{1}{2^{12} \cdot 2 \cdot \Pi \cdot 1KHz} = 39 nS $$ |
Trabajo Práctico Nro.6 Adaptación de señales y cálculo de ADC
Ejercicio 1
Se desea leer con un ADC una señal que varía entre -2 y 2 V, el ADC posee una entrada de 0 a 5 V, realizar el circuito de adaptación de señal.
Solución
La entrada del amplificador, varia entre -2 y 2 V esto da un rango de 4V a la entrada, por otro lado, la salida está dada por los 5V de amplitud máxima del ADC.
Planteamos un circuito amplificador sumador no inversor, a la señal le sumamos 2 V, necesarios para que la señal luego de amplificarla, varíe entre 0 y 5 V evitando así entrada negativa al ADC
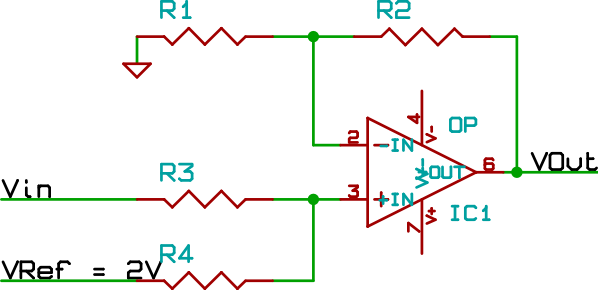
Ecuaciones del amplificador, el cálculo de las resistencia se realiza suponiendo que el paralelo entre R1 y R2 es el mismo que R3 y R4
En el caso de la máxima entrada por Vin tendremos:
estamos considerando ambas ramas con la misma amplificación, por lo tanto podemos igualar las resistencias R4 = R3
Buscamos una relación de resistencias de 5/4.
Se puede elegir entonces
Ejercicio 2
Se desea medir una señal que varíe entre 0 y 2 V, con una resolución de 0,5 mV, Calcular ADC y amplificador.
Solución
En primer lugar determinamos el ADC a usar, sabemos que la señal varía entre 0 y 2 V, o sea, su rango es de 2 V, teniendo en cuenta el paso de 0,5mV, el ADC a usar deberá tener:
Cálculo del ADC e
el valor entero mas cercano es 12 bits o 4096 cuentas.
Teniendo este valor de cuentas, deberemos calcular la ganancia para que en el momento del máximo valor (2V) la salida del ADC sea 4000.
Suponemos una V de referencia para el ADC de 5 V
Tenemos entonces que el paso del ADC es de
Tomando el paso que posee nuestro sensor de 0,5mV, la ganancia será:
Ejercicio 3
Se desea medir una señal que varíe entre 0 y 3 V, con una resolución de 0,5 mV, Calcular ADC y amplificador
Solución
En primer lugar determinamos el ADC a usar, sabemos que la señal varía entre 0 y 3V, o sea, su rango es de 3 V, teniendo en cuenta el paso de 0,5mV, el ADC a usar deberá tener:
Cálculo del ADC
el valor entero mas cercano es 13 bits o 8192 cuentas.
Cálculo de ganancia para que en el momento del máximo valor (3V) la salida del ADC sea 6000.
Suponemos una V de referencia para el ADC de 5 V
Tenemos entonces que el paso del ADC es de
Tomando el paso que posee nuestro sensor de 0,5mV, la ganancia será:
Ejercicio 4
Se desea medir una señal que varíe entre -1 y 1 V, con una resolución de 0,1 mV, Calcular ADC y amplificador
Solución
La señal varía entre -1 y 1, o sea, su rango es de 2 V, teniendo en cuenta el paso de 0,1mV, el ADC a usar deberá tener:
Cálculo del ADC
el valor entero mas cercano es 15 bits o 32768 cuentas
Teniendo este valor de cuentas, deberemos calcular la ganancia para que en el momento del máximo valor (2) la salida del ADC sea 20000.
Suponemos una V de referencia para el ADC de 3,5 V
Tenemos entonces que el paso del ADC es de
Tomando el paso que posee nuestro sensor de 0,1mV, la ganancia será:
Otra forma es modificar levemente la tensión de referencia, y de esta forma evitar el uso de un amplificador.
Ejercicio 5
Una balanza de rango 0 a 5Kg, es medida con un ADC de 12 bis de resolución, calcule el menor paso posibles en números enteros de gramos.
Solución
una resolución de 12 bits equivale a 4096 cuentas, este valor implica un salto de
El valor entero mas cercano es 2 g
Ejercicio 6
En el Ejercicio 3, determinar los errores máximos admisibles en la tensión de referencia y la ganancia del amplificador.
Solución
Los errores de tensión de referencia y ganancia están relacionados con el como el valor del LSB (Least Significant Bit), en ambos casos no debe ser superior a 1/4 del mismo
El error calculado corresponde a la máxima desviación admisible en cada etapa. En el caso de la tensión de referencia la máxima desviación sera ocasionada por la tensión de ripple, por lo tanto
En cambio, el error de ganancia se determina como la relación entre el error máximo y la Vref.
o un valor un poco mas optimista calculando el error con la máxima salida del amplificador.
Ejercicio 7
Del Ejercicio 4, determinar los errores máximos admisibles en la tensión de referencia y la ganancia del amplificador.
Solución
Los errores de tensión de referencia y ganancia están relacionados con el como el valor del LSB (Least Significant Bit), en ambos casos no debe ser superior a 1/4 del mismo
El error de la tensión de referencia será:
Error de ganancia
De nuevo calculamos el error de ganancia en el rango que utilizaremos el amplificador
Ejercicio 8
Se dispone de una señal a medir cuya componente armónica mas elevada es de 1KHz, determinar tiempo máximo de conversión y tiempo máximo de muestreo
Solución
Para calcular el tiempo máximo de conversión, deberemos determinar primero la frecuencia de muestreo.
La misma por el teorema de muestreo deberá ser al menos 2 veces la frecuencia a muestrear, a fines prácticos tomamos 5 veces la frecuencia de la señal.
El tiempo de conversión será entonces
Para evitar error en la toma de la señal, calculamos el máximo tiempo de muestreo, este tiempo deberá ser tal, que en el momento de mayor crecimiento de la señal, la misma, no varíe mas de un cierto error e.
Calculamos la variación de la señal sinusoidal en el momento de mayor crecimiento.
Derivamos la señal
Tomando la máxima derivada y en un entorno muy pequeño podemos reemplazar al cos por 1
Expresamos ahora en función de la frecuencia y despejamos la variación de tensión
El error lo definimos como el cociente entre la variación de tensión y el valor pico a pico
El error calculado deberá ser menor a medio bit.
finalmente calculamos el ts en función del salto de bit y a la frecuencia
En el caso del problema planteado y tomando un ADC ejemplo de 12 bits, el tiempo de muestreo deberá ser como máximo
