Bienvenido: Ingresar

Subir página de contenido

Puedes subir contenido para la página con el nombre abajo. Si cambias el nombre de la página, puedes subir contenido para otra página. Si el nombrede la página lo dejas en blanco, tomaremos el nombre del archivo

Archivo de contenido para la página
Nombre de la página
Comentario
En el juego de las bochas, como se llama la mas chiquita?

location: WebHome / TrabajosPracticos / PracticoADC7

$ \alpha $ is alpha

Trabajo Práctico Nro.4 Adaptación de señales y cálculo de ADC

Ejercicio 1

Se desea leer con un ADC una señal que varía entre -2 y 2 V, el ADC posee una entrada de 0 a 5 V, realizar el circuito de adaptación de señal.

Solución

La entrada del amplificador, varia entre -2 y 2 V esto da un rango de 4V a la entrada, por otro lado, la salida está dada por los 5V de amplitud máxima del ADC.

$ y^2 \over 2 $

$G = \frac{\Delta Vout}{\Delta Vin} = \frac{5}{4} = 1,25$ 

    ΔVout      5 
G =-------- = --- = 1,25
    ΔVin       4

Planteamos un circuito amplificador sumador no inversor, a la señal le sumamos 2 V, necesarios para que la señal luego de amplificarla, varíe entre 0 y 5 V evitando así entrada negativa al ADC

"Pr5_1.png"

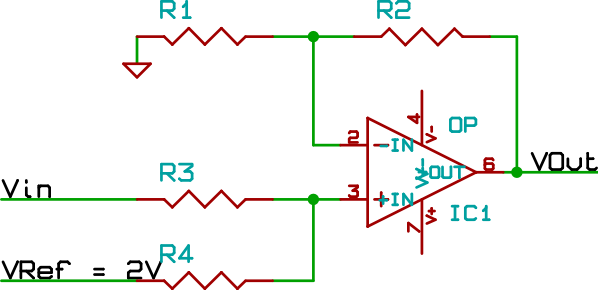
Ecuaciones del amplificador, el cálculo de las resistencia se realiza suponiendo que el paralelo entre R1 y R2 es el mismo que R3 y R4.

$$Vo = \frac{R2}{R3}Vin +\frac{R2}{R4} VRef$

En el caso de la máxima entrada por Vin tendremos:

$$5 = \frac{R2}{R3}2 + \frac{R2}{R4}2$

estamos considerando ambas ramas con la misma amplificación, por lo tanto podemos igualar las resistencias R4 = R3

$$5 = \frac{R2}{R3}4$

$$\frac{R2}{R3} = \frac{5}{4}$

Buscamos una relación de resistencias de 5/4.

Se puede elegir entonces

$$R1,R2 = 15K\Omega$ $$R3,R4 = 12K\Omega$

Ejercicio 2

Se desea medir una señal que varíe entre 0 y 2 V, con una resolución de 0,5 mV, Calcular ADC y amplificador.

Solución

En primer lugar determinamos el ADC a usar, sabemos que la señal varía entre 0 y 2 V, o sea, su rango es de 2 V, teniendo en cuenta el paso de 0,5mV, el ADC a usar deberá tener:

$$cuentas = \frac{2}{0,5\times10^{-3}} = 4000$ 

            2       
cuentas =------------ = 4000
          0,5x10^-3

Cálculo del ADC e

$$2^n = 4000$

$$n\log{2} = \log{4000}$

$$n=\frac{\log{4000}}{\log{2}}=11,965784285 $ 

2^n = 4000
n log(2) = log(4000)

      log(4000)       
n = ------------ = 11,965784285
      log(2)

el valor entero mas cercano es 12 bits o 4096 cuentas.

Teniendo este valor de cuentas, deberemos calcular la ganancia para que en el momento del máximo valor (2V) la salida del ADC sea 4000.

Suponemos una V de referencia para el ADC de 5 V

Tenemos entonces que la resolución en tensión del ADC es de 

           5    
  Vlsb = ----- = 1,220703 mV
          4096


       Vlsb     1,220703 x 10^-3
  G = ------ = ------------------ = 2,441406 
        Vs        0,5 x 10^-3

$$ V_{lsb}= \frac{5V}{4096} = 1,220703 mV$

Tomando el paso que posee nuestro sensor de 0,5mV, la ganancia será:

$$G = \frac{V_{lsb}}{V_s} = \frac{1,220703\times10^{-3}}{0,5\times10^{-3}} = 2,441406 $

Práctico a Desarrollar

Pagina con las soluciones (SOLUCIONES)

Ejercicio 1

Se desea medir una señal que varíe entre 0 y 3 V, con una resolución de 0,5 mV, Calcular ADC y amplificador

Ejercicio 2

Se desea medir una señal que varíe entre -1 y 1 V, con una resolución de 0,1 mV, Calcular ADC y amplificador

Ejercicio 3

Una balanza de rango 0 a 5Kg, es medida con un ADC de 12 bis de resolución, calcule el menor paso posibles en números enteros de gramos.

Ejercicio 4

En el Ejercicio 1, determinar los errores máximos admisibles en la tensión de referencia y la ganancia del amplificador.

Ejercicio 5

Del Ejercicio 2, determinar los errores máximos admisibles en la tensión de referencia y la ganancia del amplificador.

Ejercicio 8

Se dispone de una señal a medir cuya componente armónica mas elevada es de 1KHz, determinar tiempo máximo de conversión y tiempo máximo de muestreo