Diferencias para "LabElectronica/ProyectoQuadricoptero/PVTOL_ControlDelAngulo" - CIII UTN-FRC

Bienvenido:

location: Diferencias para "LabElectronica/ProyectoQuadricoptero/PVTOL_ControlDelAngulo"

Diferencias entre las revisiones 1 y 5 (abarca 4 versiones)

Modelo Balancín

$$G_p = \frac{K_J}{s^2}$

$$$G_c = K_p$$

$$K_M = \frac{\Delta_F}{\Delta_D}$

$$K_J = \frac{r}{J_T}$

En donde

$$G_c$$

es el compensador,

$$k_M$$

es la función de transferencia entre fuerza y duty, y

$$k_J$$

es la función de transferencia entre fuerza y ángulo.

$$r$$

representa la distancia desde la aplicación de la fuerza hasta el centro de giro y

$$J_T$$

es la inercia total.

La función de transferencia a Lazo abierto queda:

$$G_{LA}(s) = \frac{K_pK_MK_J}{s^2}$

Modelo Balancín con Compensación Proporcional y Realimentación

Suponemos que la función de transferencia del sensor es lineal, por esto podemos decir que la

$$H(s)=1$$

.

De esto obtenemos:

$$\frac{\Phi_{ref}(s)}{\Phi_{Med}(s)}=\frac{G_{LA}(s)}{1+G_{LA}(s)H(s)}=\frac{K_pK_MK_J}{s^2 + K_pK_MK_J}$

Modelo Balancín con Compensación Proporcional-Derivativa y Realimentación

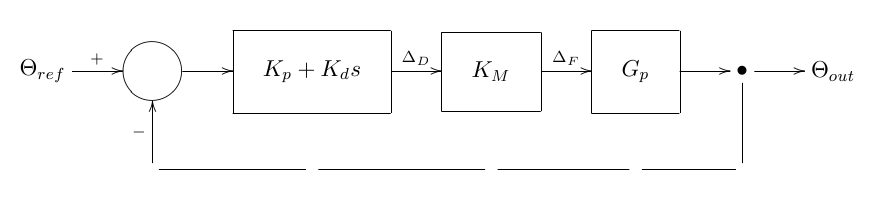
Suponemos que la función de transferencia del sensor es lineal, por esto podemos decir que la

$$H(s)=1$$

.

De esto obtenemos:

$$$G_c(s) = K_p + K_ds$$

$$G_{LA}(s) = \frac{K_MK_J}{s^2}$

$$\frac{\Phi_{ref}(s)}{\Phi_{Med}(s)}=\frac{G_{LA}(s)G_c(s)}{1+G_{LA}(s)H(s)G_c(s)}=\frac{K_pK_MK_J + K_dK_MK_Js}{s^2 + K_dK_MK_Js + K_pK_MK_J}$

Cálculo Aproximado de las constantes

Cálculo de la constante de Inercia

$$J = \sum{m.r^2}$

$$J_T = 2(J_{motor} + J_{ESC} + J_{helice}) + J_{barra}$

$$J_{motor} = 52.{20,5}^2 [g.{cm}^2] = 21853 [g.{cm}^2]$

$$J_{ESC} = 32.{10}^2 [g.{cm}^2] = 3200 [g.{cm}^2]$

$$J_{helice} = 15.{20,5}^2 [g.{cm}^2] = 6303,75 [g.{cm}^2]$

$$J_{barra} = \frac{m.L^2}{12} = \frac{110.{51}^2}{12} [g.{cm}^2] = 23842,5 [g.{cm}^2]$

$$J_T = 86556 [g.{cm}^2]$

None: LabElectronica/ProyectoQuadricoptero/PVTOL_ControlDelAngulo (última edición 2010-09-24 23:27:14 efectuada por Jaarac)