Tabla de Contenidos
- Modelo Balancín
- Modelo Balancín con Compensación Proporcional y Realimentación
- Modelo Balancín con Compensación Proporcional-Derivativa y Realimentación
- Modelo Balancín con Compensador PID
- Cálculo Aproximado de las constantes
- Análisis Discreto
- Análisis en tiempo continuo, con retentor de orden cero aproximado
- Diseño del Controlador PID Discreto para el Balancín
- Diseño del Controlador PI PD para el Balancín
Modelo Balancín
Correcciones: la referencia a lazo abierto no es ángulo, debería ser torque. |

En donde
es el compensador,
es la función de transferencia entre fuerza y duty, y
es la función de transferencia entre fuerza y ángulo.
representa la distancia desde la aplicación de la fuerza hasta el centro de giro y
es la inercia total.
La función de transferencia a Lazo abierto queda:
Modelo Balancín con Compensación Proporcional y Realimentación
Suponemos que la función de transferencia del sensor es lineal, por esto podemos decir que la
.
De esto obtenemos:
Modelo Balancín con Compensación Proporcional-Derivativa y Realimentación
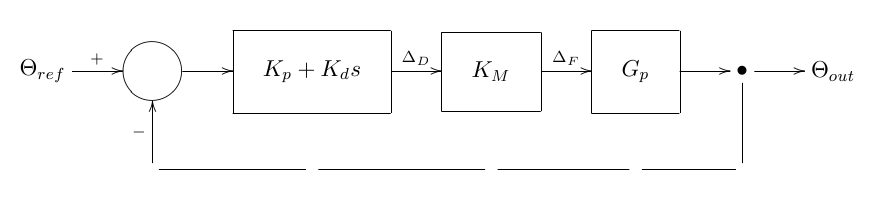
Suponemos que la función de transferencia del sensor es lineal, por esto podemos decir que la
.
De esto obtenemos:
Modelo Balancín con Compensador PID
;
.
Cálculo Aproximado de las constantes
Cálculo de la constante de Inercia
Cálculo de la constante del Motor
Según las mediciones realizadas podemos aproximar estas constantes.
Estabilización en modo común
En esta medición se trato de llevar el ángulo del PVTOL a cero seteando el pwm de un motor y ajustando el otro para que el ángulo sea 0.
Motor Normal |
Motor Pusher |
7700 |
5750 |
8350 |
7600 |
10100 |
11150 |
11750 |
14200 |
Análisis Discreto
Correcciones: El bloque del retentor de orden cero va después del bloque del compensador |

Planta:
Retentor de Orden Cero:
Análisis en tiempo continuo, con retentor de orden cero aproximado
Una aproximación de esto es
Diseño del Controlador PID Discreto para el Balancín
Funciones de Transferencia
Función de Transferencia de la Planta más el Retentor de Orden Cero
Tiempo Continuo
Una aproximación de esto es
, pero no la usaremos.
Tiempo Discreto
Función de Transferencia del Controlador PID
Tiempo Discreto
Función de Transferencia a Lazo Abierto
Tiempo Discreto
Si definimos
y
.
Función de Transferencia a Lazo Cerrado
Tiempo Discreto
Definiendo
y
como en el punto anterior y definiendo
y
.
Diseño del Controlador PI PD para el Balancín
Planta
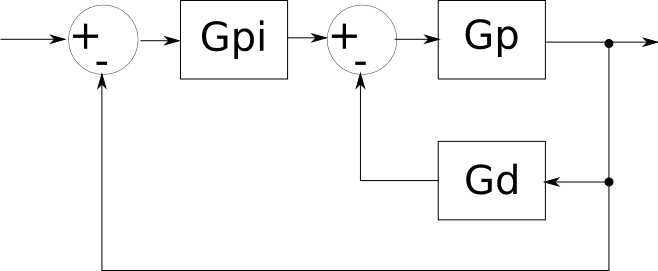
Función de Transferencia a Lazo Abierto
Función de Transferencia a Lazo Cerrado
Análisis suponiendo ti = 0
Polos de la función de transferencia a lazo cerrado.
Vemos que los polos arrancan sobre el eje sigma negativo y a medida que aumentamos k se acercan entre ellos hasta que se juntan en un punto de ruptura en el eje sigma negativo y empiezan a ser complejos conjugados. El punto de ruptura depende del valor de kd, a medida que este aumenta este punto de ruptura se mueve hacia la izquierda.

