|
Tamaño: 1959
Comentario:
|
Tamaño: 2694
Comentario:
|
| Los textos eliminados se marcan así. | Los textos añadidos se marcan así. |
| Línea 1: | Línea 1: |
| ## page was renamed from LabElectronica/PVTOL_ControlDelAngulo | |
| Línea 2: | Línea 3: |
| ##Borrar esta linea y dejar la siguiente que permite que ésta página sea pública #acl BecariosGrupo:read,write,admin All:read |
#acl BecariosGrupo:read,write,admin,delete All:read <<TableOfContents(6)>> |
| Línea 30: | Línea 33: |
{{attachment:FdTLA_PD.png || width="600"}} |
|
| Línea 42: | Línea 48: |
$$$K_J = \frac{r}{J_T}$$ |
|
| Línea 55: | Línea 64: |
$$$\boxed{K_J = \frac{21}{86556}[\frac{1}{g.cm}]}$$ === Cálculo de la constante del Motor === Según las mediciones realizadas podemos aproximar estas constantes. $$$K_{MPusher} = \frac{\Delta_F}{\Delta_D} = \frac{40}{3000}\frac{g}{cuentas}$$ $$$K_{MNormal} = \frac{\Delta_F}{\Delta_D} = \frac{70}{3000}\frac{g}{cuentas}$$ ==== Estabilización en modo común ==== En esta medición se trato de llevar el ángulo del PVTOL a cero seteando el pwm de un motor y ajustando el otro para que el ángulo sea 0. || Motor Normal || Motor Pusher || || 7700 || 5750 || || 8350 || 7600 || || 10100 || 11150 || || 11750 || 14200 || |
Tabla de Contenidos
Modelo Balancín

En donde
es el compensador,
es la función de transferencia entre fuerza y duty, y
es la función de transferencia entre fuerza y ángulo.
representa la distancia desde la aplicación de la fuerza hasta el centro de giro y
es la inercia total.
La función de transferencia a Lazo abierto queda:
Modelo Balancín con Compensación Proporcional y Realimentación
Suponemos que la función de transferencia del sensor es lineal, por esto podemos decir que la
.
De esto obtenemos:
Modelo Balancín con Compensación Proporcional-Derivativa y Realimentación
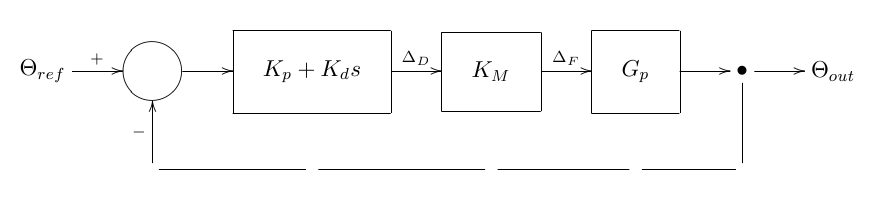
Suponemos que la función de transferencia del sensor es lineal, por esto podemos decir que la
.
De esto obtenemos:
Cálculo Aproximado de las constantes
Cálculo de la constante de Inercia
Cálculo de la constante del Motor
Según las mediciones realizadas podemos aproximar estas constantes.
Estabilización en modo común
En esta medición se trato de llevar el ángulo del PVTOL a cero seteando el pwm de un motor y ajustando el otro para que el ángulo sea 0.
Motor Normal |
Motor Pusher |
7700 |
5750 |
8350 |
7600 |
10100 |
11150 |
11750 |
14200 |

