Bienvenido: Ingresar

Subir página de contenido

Puedes subir contenido para la página con el nombre abajo. Si cambias el nombre de la página, puedes subir contenido para otra página. Si el nombrede la página lo dejas en blanco, tomaremos el nombre del archivo

Archivo de contenido para la página
Nombre de la página
Comentario
En el juego de las bochas, como se llama la mas chiquita?

Versión 32 con fecha 2010-10-04 13:06:01

location: LabElectronica / ProyectoQuadricoptero / QA3Fase1EstModYConArqRobMoviles / Balancin

Tabla de Contenidos

  1. Modelo Balancín con Compensador PID
    1. Modelo Continuo
      1. Archivos para Simulaciones
    2. Modelo Discreto

Modelo Balancín con Compensador PID

Modelo Continuo

planta_lc_continuo.png

$$$ \sum{\tau_x} = \tau_2 - \tau_1 = J\frac{d^2\theta}{dt^2} $$

$$$ s^2\theta_{(s)}= \frac{\tau_{(s)}}{J} $$

$$$ G_{bal(s)} = \frac{1}{Js^2} $$

$$$ G_{torque(s)} = k_\tau $$

$$$ G_{PID(s)} = k_p\cdot(1 + \frac{1}{T_is} + T_ds}) $$

$$$ G_{LA(s)} = G_{bal(s)}G_{torque(s)}G_{PID(s)} = \frac{k_pk_\tau}{T_iJ}\frac{T_iT_ds^2 + T_is + 1}{s^3} $$

$$$ G_{LC(s)} = \frac{G_{LA(s)}}{1+G_{LA(s)}} = k_pk_\tau\frac{T_iT_ds^2 + T_is + 1}{T_iJs^3 + k_pk_\tauT_iT_ds^2 + k_pk_\tauT_is + k_pk_\tau}$$

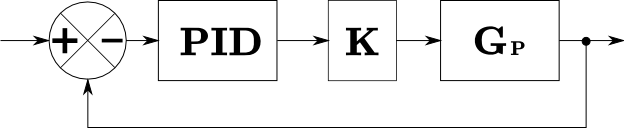
Archivos para Simulaciones

   1 J = 0.0086556;
   2 Kp = 1;
   3 Kt = 90.63e-6;
   4 Ti = 0;
   5 Td = 0;
   6 
   7 desicion = 1;
   8 
   9 while( desicion == 1)
  10 
  11 	%Kp = input('Ingrese Kp : ');
  12 	Ti = input('Ingrese Ti : ');
  13 	Td = input('Ingrese Td : ');
  14 
  15 	num = Kp*Kt/(Ti*J)*[Ti*Td, Ti, 1];
  16 	den = [1, 0, 0, 0];
  17 
  18 	sistema = tf(num,den);
  19 
  20     K_inc = input('Ingrese el incremento de K del rlocus: ');
  21 	K_max = input('Ingrese el K_max del rlocus: ');
  22 	
  23 	%rlocus(sistema,K_inc,0,K_max);
  24     rlocus(sistema);
  25 
  26     pause;
  27 	desicion = input('Ingrese 1 para hacer otro rlocus: ');
  28 
  29 end

PID_LA_continuo.m

Modelo Discreto

planta_lc_discreto.png

$$$ G_{bal(s)} = \frac{1}{Js^2} $$

$$$ G_{ROC(s)}=\frac{1-e^{-TS}}{S}$$

$$$ G_{torque(s)} = k_\tau $$

$$$ G_{PID(s)} = k_p\cdot(1 + \frac{1}{T_is} + T_ds}) $$

$$$ G_{planta(Z)} = Z[G_{ROC(s)}G_{bal(s)}G_{torque(s)}] = Z[\frac{1 - e^{-TS}}{S}\frac{k_\tau}{JS^2}] = (1-z^-1)Z[\frac{2k_\tau}{2JS^3}] = \frac{T^2k_\tau}{2J}\frac{z+1}{z^2-2z+1}$$

$$$ G_{PID(Z)} = K_P + \frac{K_I}{1-z^-1} + K_D(1-z^-1) = \frac{(K_P + K_I + K_D)z^2 + ( -2K_D - K_P )z + K_D }{ z^2 - z } $$

$$$ G_{LA(Z)} = G_{PID(Z)}G_{planta(Z)} = \frac{T^2k_\tau}{2J}\frac{(K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D}{z^4-3z^3+3z^2-z} $$

$$$ G_{LC(Z)} = \frac{G_{LA(Z)}}{1+G_{LA(Z)}} = \frac{k_{\tau}T^2((K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D)}{ 2Jz^4 + ((K_P + K_I + K_D)k_{\tau}T^2 -6 )z^3 + ((K_I - K_D)k_{\tau}T^2 +6 )z^2 + ( ( -K_P - K_D ) k_{\tau} T^2 -2 )z + K_D k_{\tau} T^2 } $$