Bienvenido: Ingresar

No tienes permisos para la acción RecommendPage en esta página.

Quitar mensaje
location: LabElectronica / ProyectoQuadricoptero / QA3Fase1EstModYConArqRobMoviles / Balancin

Estudio del modelo del Balancín y de su compensador

Tabla de Contenidos

  1. Estudio del modelo del Balancín y de su compensador
    1. Compensador PID
      1. Ecuacion Diferencial
      2. Transformada de Laplace
      3. Transformada Z
      4. Tiempo Discreto
    2. Modelo Balancín con Compensador PID
      1. Modelo Continuo
        1. Archivos para Simulaciones
      2. Modelo Discreto
        1. Archivos para Simulaciones

Compensador PID

Ecuacion Diferencial

$$$ c(t) = k[e(t) + \frac{1}{T_i}\int_0^t \! e(t) dt \ + T_d \frac{de(t)}{dt} ] $$

Transformada de Laplace

$$$ C(s) = k( 1 + \frac{1}{T_i s} + T_d s ) E(s) $$

Transformada Z

$$$ C(z) = k[1-\frac{T}{2T_i} + \frac{T}{T_i}\frac{1}{1-z^{-1}} + \frac{T_d}{T}(1-z^{-1}) ]E(z) $$

$$$ C(z) = [K_p + \frac{K_i}{1-z^{-1}} + K_d(1-z^{-1}) ]E(z) $$

Tiempo Discreto

$$$ c(k) = c(k-1) + K_p[e(k)-e(k-1)] + K_i e(k) + K_d[e(k)-2e(k-1)+e(k-2)] $$

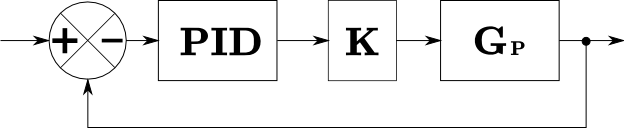
Modelo Balancín con Compensador PID

Modelo Continuo

planta_lc_continuo.png

$$$ \sum{\tau_x} = \tau_2 - \tau_1 = J\frac{d^2\theta}{dt^2} $$

$$$ s^2\theta_{(s)}= \frac{\tau_{(s)}}{J} $$

$$$ G_{bal(s)} = \frac{1}{Js^2} $$

$$$ G_{torque(s)} = k_\tau $$

$$$ G_{PID(s)} = k_p\cdot(1 + \frac{1}{T_is} + T_ds}) $$

$$$ G_{LA(s)} = G_{bal(s)}G_{torque(s)}G_{PID(s)} = \frac{k_pk_{\tau}}{T_iJ}\frac{T_iT_ds^2 + T_is + 1}{s^3} $$

$$$ G_{LC(s)} = \frac{G_{LA(s)}}{1+G_{LA(s)}} = k_p k_{\tau} \frac{T_i T_d s^2 + T_i s + 1}{T_i J s^3 + k_p k_{\tau} T_i T_d s^2 + k_p k_{\tau} T_i s + k_p k_{\tau}}$$

Archivos para Simulaciones

Simulacion de la planta a lazo abierto con el PID. 

   1 J = 0.0086556;
   2 Kp = 1;
   3 Kt = 90.63e-6;
   4 Ti = 0;
   5 Td = 0;
   6 
   7 desicion = 1;
   8 
   9 while( desicion == 1)
  10 
  11 	%Kp = input('Ingrese Kp : ');
  12 	Ti = input('Ingrese Ti : ');
  13 	Td = input('Ingrese Td : ');
  14 
  15 	num = Kp*Kt/(Ti*J)*[Ti*Td, Ti, 1];
  16 	den = [1, 0, 0, 0];
  17 
  18 	sistema = tf(num,den);
  19 
  20     K_inc = input('Ingrese el incremento de K del rlocus: ');
  21 	K_max = input('Ingrese el K_max del rlocus: ');
  22 	
  23 	%rlocus(sistema,K_inc,0,K_max);
  24     rlocus(sistema);
  25 
  26     pause;
  27 	desicion = input('Ingrese 1 para hacer otro rlocus: ');
  28 
  29 end
PID_LA_continuo.m

Respuesta en el tiempo de la planta a lazo cerrado con el PID. 

   1 J = 8.56e-3
   2 td=.1;
   3 ti=1e9;
   4 kt = 90.63e-6;
   5 kp = 10000;
   6 step(tf(kp*kt*[td*ti,ti,1],[ti*J,ti*td*kp*kt,kp*kt*ti,kp*kt]),1,1,100);
   7 ylabel("respuesta al escalon con PID");
PID_LC_continuo.m

Modelo Discreto

planta_lc_discreto.png

$$$ G_{bal(s)} = \frac{1}{Js^2} $$

$$$ G_{ROC(s)}=\frac{1-e^{-TS}}{S}$$

$$$ G_{torque(s)} = k_\tau $$

$$$ G_{PID(s)} = k_p\cdot(1 + \frac{1}{T_is} + T_ds}) $$

$$$ G_{planta(Z)} = Z[G_{ROC(s)}G_{bal(s)}G_{torque(s)}] = Z[\frac{1 - e^{-TS}}{S}\frac{k_\tau}{JS^2}] = (1-z^-1)Z[\frac{2k_\tau}{2JS^3}] = \frac{T^2k_\tau}{2J}\frac{z+1}{z^2-2z+1}$$

$$$ G_{PID(Z)} = K_P + \frac{K_I}{1-z^-1} + K_D(1-z^-1) = \frac{(K_P + K_I + K_D)z^2 + ( -2K_D - K_P )z + K_D }{ z^2 - z } $$

$$$ G_{LA(Z)} = G_{PID(Z)}G_{planta(Z)} = \frac{T^2k_\tau}{2J}\frac{(K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D}{z^4-3z^3+3z^2-z} $$

$$$ G_{LC(Z)} = \frac{G_{LA(Z)}}{1+G_{LA(Z)}} = \frac{k_{\tau}T^2((K_P + K_I + K_D)z^3 + (K_I - K_D)z^2 + (-K_P - K_D)z + K_D)}{ 2Jz^4 + ((K_P + K_I + K_D)k_{\tau}T^2 -6J )z^3 + ((K_I - K_D)k_{\tau}T^2 +6J )z^2 + ( ( -K_P - K_D ) k_{\tau} T^2 -2J )z + K_D k_{\tau} T^2 } $$

Archivos para Simulaciones

Simulacion de la planta a lazo abierto con el PID. 

   1 ti = 1e9;
   2 td = .1;
   3 kt = 90.63e-6;
   4 t = 1/20000;
   5 J = 8.6556e-3;
   6  
   7 k = kt; 
   8 kp = k-k*t/(2*ti); 
   9 kd = k*td/t;
  10 ki = k*t/ti;
  11 
  12 num = t^2/(2*J)*[kd+ki+kp,-kd+ki,-kd-kp,kd];
  13 den = [1,-3,3,-1,0];
  14 
  15 hold off;
  16 rlocus(tf(num,den,t));
  17 
  18 tita = 0:0.01*pi:2*pi;
  19 x = sin(tita);
  20 y = cos(tita);
  21 hold on;
  22 plot(x,y,'o1');
PID_LA_discreto.m

Respuesta en el tiempo de la planta a lazo cerrado con el PID. 

   1 J = 8.56e-3;
   2 td=.1;
   3 ti=1e9;
   4 T=1/200;
   5 
   6 k = 1000;
   7 kt = 90.63e-6;
   8 
   9 kp = k-k*T/(2*ti);
  10 ki = k*T/ti;
  11 kd = k*td/T;
  12 
  13 num = T^2*kt*[kp+ki+kd,ki-kd,-kp-kd,kd];
  14 den = [2*J,(kp+ki+kd)*kt*T^2-6*J,(ki-kd)*kt*T^2+6*J,(-kp-kd)*kt*T^2-2*J,kd*kt*T^2];
  15 
  16 step(tf(num,den,T));
  17 
  18 ylabel("respuesta al escalon con PID");
  19 
  20 pause();
PID_LC_discreto.m