Bienvenido: Ingresar
location: Diferencias para "WebHome/TrabajosPracticos/PracticoBase1"
Diferencias entre las revisiones 2 y 4 (abarca 2 versiones)
⇤ ← Versión 2 con fecha 2010-06-01 16:07:57 →
Tamaño: 5812
Editor: TiN
Comentario:
← Versión 4 con fecha 2010-09-09 13:56:11 → ⇥
Tamaño: 5849
Editor: GuillermoSteiner
Comentario:
Los textos eliminados se marcan así. Los textos añadidos se marcan así.
Línea 1: Línea 1:
[[PracticoBase1Soluciones|EJERCICIOS RESUELTOS ]] ## page was renamed from PracticoBase1
[[/PracticoBase1Soluciones|EJERCICIOS RESUELTOS ]]
Línea 231: Línea 232:

EJERCICIOS RESUELTOS

Trabajo Práctico Nro 1 Bases Numéricas

Este práctico tiene como objetivo el repaso de las bases numéricas y las operaciones aritméticas básicas (suma y resta) realizadas en binario

Ejercicio Nro 1

  • Representar 42110 en base 2

"binario1.png"

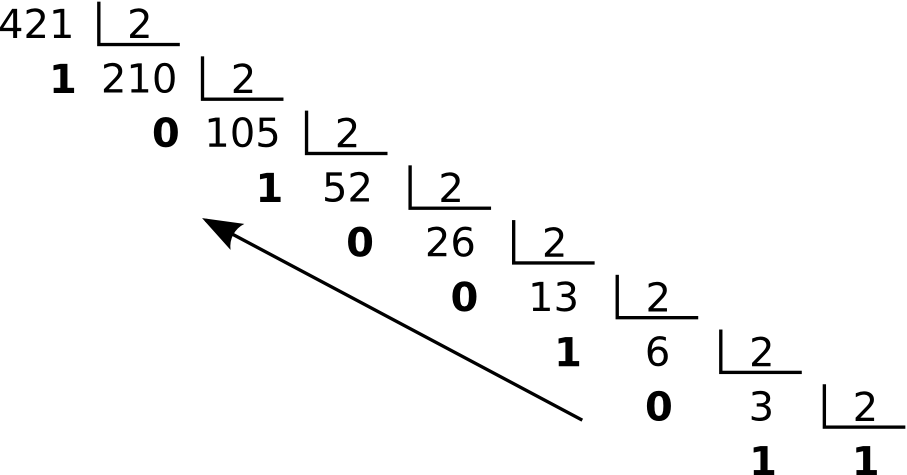
Resultado: 110100101b

Ejercicio Nro 2

Representar 110101112 en base 10

1 x 20

=

1

1 x 21

=

2

1 x 22

=

4

0 x 23

=

0

1 x 24

=

16

0 x 25

=

0

1 x 26

=

64

1 x 27

=

128

Resultado

215

Resultado: 215

Ejercicio Nro 3

Representar 1101,1012 en base 10

1 x 2-3

=

0,125

0 x 2-2

=

0

1 x 2-1

=

0,5

1 x 20

=

1

0 x 21

=

0

1 x 22

=

4

1 x 23

=

8

Resultado: 13,625

Ejercicio Nro 4

Representar 23,4310 en base 2 con 8 dígitos después de la coma.

Parte Entera

"binario2.png"

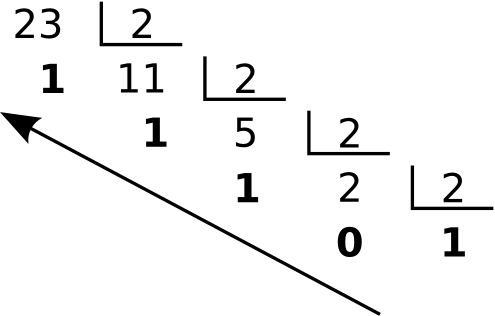
Parte Decimal

0,43 x 2

=

0,86

Entero = 0

0,86 x 2

=

1,72

Entero = 1

0,72 x 2

=

1,44

Entero = 1

0,44 x 2

=

0,88

Entero = 0

0,88 x 2

=

1,76

Entero = 1

0,76 x 2

=

1,52

Entero = 1

0,52 x 2

=

1,04

Entero = 1

0,04 x 2

=

0,08

Entero = 0

Resultado: 10111,01101110

Ejercicio Nro 5

Representar 10,2710 en base 2 con un error maximo de 0,1% 

E = 0,1 % 
e = 0,01027

2^n = 0,01027

n = ln(0,01027) / ln(2) = -6.605

tomamos el entero menor 

n = -7

Esto significa que para tener un error menor a 0,1 % deberemos tomar hasta el 7 digito

Ahora resolvemos

Parte Entera

1010

Parte Decimal

0,27 x 2

=

0,54

Entero = 0

0,54 x 2

=

1,08

Entero = 1

0,08 x 2

=

0,16

Entero = 0

0,16 x 2

=

0,32

Entero = 0

0,32 x 2

=

0,64

Entero = 0

0,64 x 2

=

1,28

Entero = 1

0,28 x 2

=

0,56

Entero = 0

Resultado: 1010,010001

Comprobación

1 x 2-6

=

0,015625

0 x 2-5

=

0

0 x 2-4

=

0

0 x 2-3

=

0

1 x 2-2

=

0,25

0 x 2-1

=

0

0 x 20

=

0

1 x 21

=

2

0 x 22

=

0

1 x 23

=

8

Resultado

* *

10,265625

El error es 

e = 10,27 - 10,265625 = 0,004375 < 0,01027

Ejercicio Nro 6

Representar los siguientes numeros con signo en formato Signo + Magnitud, Complemento a 1,Complemento a 2, Exceso de 7

Nro

Val Abs

Sig+Mag

Comp 1

Comp 2

Exc 7

-5

0101

1101

1010

1011

0010

-8

1000

x

x

1000

x

-7

0111

1111

1000

1001

0000

-3

0011

1011

1100

1101

0100

0

0000

0000 y 1000

0000 y 1111

0000

0111

7

0111

0111

0111

0111

1110

8

1000

x

x

x

1111

Ejercicio Nro 7
  • Realizar las siguientes operaciones aritméticas en base 2

Sumar (1010 0101 + 1001 0011) 

          11
   1010 0101
+
   1001 0011
 ------------
  10011 1000

Restar (1010 0101 - 1001 0011) 

           1
   1010 0101
-
   1001 0011
  -----------
   0001 0010

Otro método es:

Sacar el complemento a dos del sustraendo 

      1001 0011
 C1 = 0110 1100
    +    1. 
 C2 = 0110 1101

Sumar el minuendo al complemento a dos del sustraendo 

  •    1010 0101
+
   0110 1101
 ------------
  10001 0010

El 9 bits no se toma y nos queda el resultado final Resultado = 00010010

Práctico de Aula a Desarrollar

Ejercicio Nro 1

Representar los siguientes número en la base solicitada

  • 17458 en Decimal

  • 1849310 en Binario

  • 101010112 en Decimal

  • 1562610 en Hexadecimal

  • 34328 en Binario

  • 174610 en Octal

  • 13488216 en Binario

Ejercicio Nro 2

Representar los siguientes número en base 10 a binario, tomando 8 bit después de la coma

  • 8,12510

  • 0,310

  • 0,4210

Ejercicio Nro 3

Representar los siguientes número en base 10 a binario, con un error maximo de 0,1 %

  • 14,4510

  • 5,95510

  • 0,4710

Ejercicio Nro 4

Representar los siguientes números en base 2 a decimal

  • 1011,0011012

  • 11,10101012

  • 0,1101110012

Ejercicio Nro 5

Representar en base 2 los siguientes números con la longitud indicada

1 Byte

16 bits o Medio Word

Número en Decimal

-51

-130

-32125

Indicar cual o cuales no pueden ser representados por 1 byte

Ejercicio Nro 6

Realizar las siguientes operaciones aritméticas en base 2

Sumar 00011101 + 10110010

Restar 00101101 - 11100101

  1. Suponiendo que son números sin signos
  2. Suponiendo que son números con signo ( 8 bits)

UntitledWiki: WebHome/TrabajosPracticos/PracticoBase1 (última edición 2020-04-02 23:05:29 efectuada por GuillermoSteiner)