Diferencias entre las revisiones 7 y 12 (abarca 5 versiones)

Trabajo Práctico Nro 1 Bases Numéricas

Este práctico tiene como objetivo el repaso de las bases numéricas y las operaciones aritméticas básicas (suma y resta) realizadas en binario.

Guía de ejercicios

Descargar subido el 15 de junio de 2019.

Ejercicios ejemplos

Ejercicio Nro 1

Representar 421₁₀en base 2

"binario1.png"

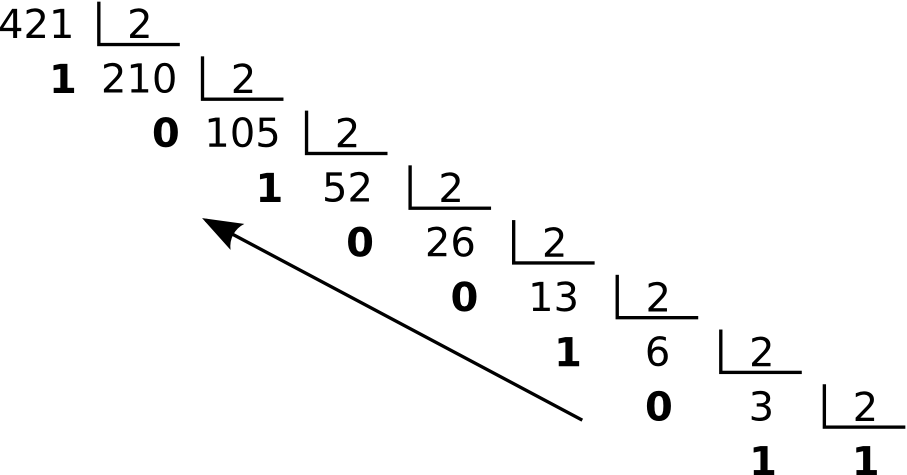
Resultado: 110100101b

Ejercicio Nro 2

Representar 11010111₂ en base 10

1 x 2⁰	=	1
1 x 2¹	=	2
1 x 2²	=	4
0 x 2³	=	0
1 x 2⁴	=	16
0 x 2⁵	=	0
1 x 2⁶	=	64
1 x 2⁷	=	128
Resultado	215

Resultado: 215

Ejercicio Nro 3

Representar 1101,101₂ en base 10

1 x 2^-3	=	0,125
0 x 2^-2	=	0
1 x 2^-1	=	0,5
1 x 2⁰	=	1
0 x 2¹	=	0
1 x 2²	=	4
1 x 2³	=	8

Resultado: 13,625

Ejercicio Nro 4

Representar 23,43₁₀ en base 2 con 8 dígitos después de la coma.

Parte Entera

"binario2.png"

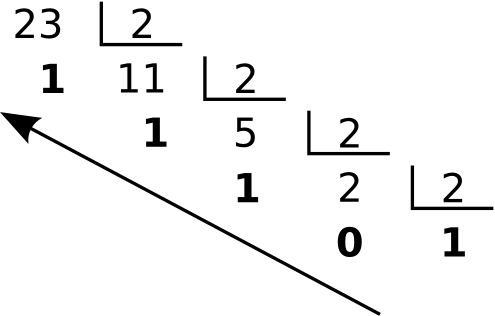
Parte Decimal

0,43 x 2	=	0,86	Entero = 0
0,86 x 2	=	1,72	Entero = 1
0,72 x 2	=	1,44	Entero = 1
0,44 x 2	=	0,88	Entero = 0
0,88 x 2	=	1,76	Entero = 1
0,76 x 2	=	1,52	Entero = 1
0,52 x 2	=	1,04	Entero = 1
0,04 x 2	=	0,08	Entero = 0

Resultado: 10111,01101110

Ejercicio Nro 5

Representar 10,27₁₀ en base 2 con un error maximo de 0,1%

E = 0,1 % 
e = 0,01027

2^n = 0,01027

n = ln(0,01027) / ln(2) = -6.605

tomamos el entero menor

n = -7

Esto significa que para tener un error menor a 0,1 % deberemos tomar hasta el 7 digito

Ahora resolvemos

Parte Entera

1010

Parte Decimal

0,27 x 2	=	0,54	Entero = 0
0,54 x 2	=	1,08	Entero = 1
0,08 x 2	=	0,16	Entero = 0
0,16 x 2	=	0,32	Entero = 0
0,32 x 2	=	0,64	Entero = 0
0,64 x 2	=	1,28	Entero = 1
0,28 x 2	=	0,56	Entero = 0

Resultado: 1010,010001

Comprobación

1 x 2^-6	=	0,015625
0 x 2^-5	=	0
0 x 2^-4	=	0
0 x 2^-3	=	0
1 x 2^-2	=	0,25
0 x 2^-1	=	0
0 x 2⁰	=	0
1 x 2¹	=	2
0 x 2²	=	0
1 x 2³	=	8
Resultado	* *	10,265625

El error es

e = 10,27 - 10,265625 = 0,004375 < 0,01027

Ejercicio Nro 6

Representar los siguientes numeros con signo en formato Signo + Magnitud, Complemento a 1,Complemento a 2, Exceso de 7

Nro	Val Abs	Sig+Mag	Comp 1	Comp 2	Exc 7
-5	0101	1101	1010	1011	0010
-8	1000	x	x	1000	x
-7	0111	1111	1000	1001	0000
-3	0011	1011	1100	1101	0100
0	0000	0000 y 1000	0000 y 1111	0000	0111
7	0111	0111	0111	0111	1110
8	1000	x	x	x	1111

Ejercicio Nro 7

Realizar las siguientes operaciones aritméticas en base 2

Sumar (1010 0101 + 1001 0011)

          11
   1010 0101
+
   1001 0011
 ------------
  10011 1000

Restar (1010 0101 - 1001 0011)

           1
   1010 0101
-
   1001 0011
  -----------
   0001 0010

Otro método es:

Sacar el complemento a dos del sustraendo

      1001 0011
 C1 = 0110 1100
    +    1. 
 C2 = 0110 1101

Sumar el minuendo al complemento a dos del sustraendo

   1010 0101
+
   0110 1101
 ------------
  10001 0010

El 9 bits no se toma y nos queda el resultado final Resultado = 00010010

Ejercicios Resueltos

Página con las soluciones (SOLUCIONES)

UntitledWiki: WebHome/TrabajosPracticos/PracticoBase1 (última edición 2020-04-02 23:05:29 efectuada por GuillermoSteiner)

-  ⇤ ← Versión 7 con fecha 2013-05-13 14:35:29 → 
  Tamaño: 5928
  Editor: GuillermoSteiner
  Comentario:
+   ← Versión 12 con fecha 2019-06-15 14:11:42 → ⇥
  Tamaño: 6106
  Editor: EstefaniaPereyra
  Comentario:
-Los textos eliminados se marcan así.
+Los textos añadidos se marcan así.
 Línea 7:
+== Guía de ejercicios ==
[[attachment:tp1.pdf|Descargar]] subido el 15 de junio de 2019.

== Ejercicios ejemplos ==
-Línea 183:
+Línea 186:
-==== Práctico de Aula a Desarrollar ====
+== Ejercicios Resueltos ==
-Línea 187:
+Línea 190:
-===== Ejercicio Nro 1 =====
Representar los siguientes número en la base solicitada 

   * 1745,,8,, en Decimal 
   * 18493,,10,, en Binario 
   * 10101011,,2,, en Decimal 
   * 15626,,10,, en Hexadecimal
   * 3432,,8,, en Binario
   * 1746,,10,, en Octal
   * 134882,,16,, en Binario
===== Ejercicio Nro 2 =====
Representar los siguientes número en base 10 a binario, tomando 8 bit después de la coma
   * 8,125,,10,,
   * 0,3,,10,,
   * 0,42,,10,,

===== Ejercicio Nro 3 =====
Representar los siguientes número en base 10 a binario, con un error maximo de 0,1 %
   * 14,45,,10,,
   * 5,955,,10,,
   * 0,47,,10,,
+##===== Ejercicio Nro 1 =====
##Representar los siguientes número en la base solicitada 

##   * 1745,,8,, en Decimal 
##   * 18493,,10,, en Binario 
##   * 10101011,,2,, en Decimal 
##   * 15626,,10,, en Hexadecimal
##   * 3432,,8,, en Binario
##   * 1746,,10,, en Octal
##   * 134882,,16,, en Binario
##===== Ejercicio Nro 2 =====
##Representar los siguientes número en base 10 a binario, tomando 8 bit después de la coma
##   * 8,125,,10,,
##   * 0,3,,10,,
##   * 0,42,,10,,

##===== Ejercicio Nro 3 =====
##Representar los siguientes número en base 10 a binario, con un error maximo de 0,1 %
##   * 14,45,,10,,
##   * 5,955,,10,,
##   * 0,47,,10,,
-Línea 209:
+Línea 212:
-===== Ejercicio Nro 4 =====
Representar los siguientes números en base 2 a decimal
   * 1011,001101,,2,,
   * 11,1010101,,2,,
   * 0,110111001,,2,,

===== Ejercicio Nro 5 =====
Representar en base 2 los siguientes números con la longitud indicada 

|| '''1 Byte''' || '''16 bits o Medio Word''' || '''Número en Decimal''' ||
||            ||                                   || -51 ||
||            ||                                   || -130 ||
||            ||                                   || -32125 ||

Indicar cual o cuales no pueden ser representados por 1 byte 

===== Ejercicio Nro 6 =====
Realizar las siguientes operaciones aritméticas en base 2

Sumar 00011101 + 10110010

Restar 00101101 - 11100101

    1. Suponiendo que son números sin signos 
    1. Suponiendo que son números con signo ( 8 bits)
+##===== Ejercicio Nro 4 =====
##Representar los siguientes números en base 2 a decimal
##   * 1011,001101,,2,,
##   * 11,1010101,,2,,
##   * 0,110111001,,2,,

##===== Ejercicio Nro 5 =====
##Representar en base 2 los siguientes números con la longitud indicada 

##|| '''1 Byte''' || '''16 bits o Medio Word''' || '''Número en Decimal''' ||
##||            ||                                   || -51 ||
##||            ||                                   || -130 ||
##||            ||                                   || -32125 ||

##Indicar cual o cuales no pueden ser representados por 1 byte 

##===== Ejercicio Nro 6 =====
##Realizar las siguientes operaciones aritméticas en base 2

##Sumar 00011101 + 10110010

##Restar 00101101 - 11100101

##    1. Suponiendo que son números sin signos 
##    1. Suponiendo que son números con signo ( 8 bits)

Buscar

Herramientas