Tabla de Contenidos
- Construcción de un Quadricóptero de Arquitectura Abierta
- Diseño del Cuadrotor
- Modelado del Quadrotor
- Filtro Complementario para la Estimación del ángulo de roll y de pitch
- Hardware de control
- Software
- Conclusiones
Construcción de un Quadricóptero de Arquitectura Abierta
Introducción
El siguiente Proyecto Final surge por la necesidad planteada por el Centro de Investigación en Informática para la Ingeniería de contar con una plataforma de hardware voladora para la realización de pruebas de algoritmos de navegación que surgen de diferentes trabajos doctorales de dicho centro.
Los vehículos voladores no tripulados, conocidos por sus siglas en inglés UAV (Unmanned Aerial Vehicle), pueden ser aeronaves de ala fija o rotante o incluso cohetes. Estos vehículos vuelan pilotados en forma remota o de manera autónoma. Aquellos UAV capaces de realizar vuelos estáticos como los helicópteros o los denominados cuatrirrotores, presentan particular interés para ciertas aplicaciones que requieren vuelos de baja altitud, entre obstáculos o incluso en espacios cerrados.
Los vuelos a baja altura en ambientes con obstáculos representan un alto riesgo para la vida de los pilotos, por esto que los vehículos no tripulados despiertan mucho interés en aplicaciones como inspección de edificios, inspección de líneas de distribución de energía eléctrica en alta tensión, tareas de rescate en zona de desastres o de alta montaña, filmación, etc. Otra razón por la que estos vehículos resultan atractivos es por su bajo costo de operación.
En el pasado, el uso de UAVs ha estado mayormente relacionado a aplicaciones militares. En la actualidad el interés por los sistemas UAV es creciente en la dirección de aplicaciones civiles; esto como consecuencia de la reducción de costos de las tecnologías involucradas.
En forma sintética se puede aseverar que la navegación de aeronaves implica la resolución eficiente y segura de cuatro tareas: toma de decisiones, percepción de obstáculos, estimación del estado de la aeronave (posición, velocidades y actitud) y control de la aeronave. En la actualidad, tanto en el ámbito militar como comercial, estas tareas se resuelven satisfactoriamente en tanto y en cuanto junto a los sistemas de automatización interactúan pilotos humanos complementando aquellos aspectos en que la técnica aún no está lo suficientemente avanzada, como ser la percepción y evasión de obstáculos. Aquí se encuentra el principal desafío para permitir la introducción de UAVs en espacios aéreos no restringidos.
Actualmente existen en el mercado pocos modelos comerciales de Quadricópteros, como pueden ser el Draganflyer X6, Parrot AR.Drone, Microdrones los cuales son usados en aplicaciones como: Fotografía Aerea y Video, Unidades de eliminación de explosivos, búsqueda y rescate, respuesta a desastres, asistencia, daños por fuego, ayuda a la construcción, inspección de lineas de transmisión, exploración geológica, control de cultivo, etc. Pero el costo de este tipo de artefactos y la poca flexibilidad que otorgan debido a sus arquitecturas cerradas dificultan su uso en la investigación universitaria.
Debido al creciente interés en este tipo de arquitecturas, son cada vez más las universidades y centros de investigación que están construyendo su propio cuadricóptero para realizar con ellos diferentes tipos de trabajos de investigación. Algunos ejemplos pueden ser MKTajamar, Mikrokopter. Estos últimos tienen la principal ventaja de ser más económicos que los anteriores, pero sin embargo su costo de ensamblado sigue siendo excesivo. Además estos tipos de proyectos aún no tienen la suficiente maduración para su uso en investigación y sólo son aplicables para usos hobbistas.
Ventajas de un QuadRotor
La elección de un quadrotor como plataforma experimental surge de un análisis de las ventajas que tiene este prototipo con respecto a otros UAV.
Un quadrotor es una aeronave del tipo PVTOL, esto significa que puede despegar y aterrizar en forma paralela el plano terrestre, lo cual nos da una gran ventaja para la navegación en ambientes interiores.
Desde el punto de vista mecánico en un QuadRotor las únicas partes móviles son las hélices. Dado que estas están acopladas directamente a los ejes de los motores no es necesario implementar ningún tipo de mecanismo. Esto es un punto a favor bastante grande ya que nuestro conociento en mecánica no es suficiente para encarar la construcción de un dispositivo con una estructura más sofisticada.
Otra ventaja interesante del QuadRotor en términos de simplicidad es la cancelación de torque total que se obtiene (ya que 2 motores giran hacia un lado y 2 hacia otro). Esto nos permite dejar de lado consideraciones respecto a la estabilización del dispositivo en el eje vertical.
También al tener cuatro hélices dispuestas el diseño del sistema de control se simplifica, permitiendo realizar un desacoplamiento de las variables.
Definición de la problemática
El principal problema de los modelos comerciales mencionados anteriormente es que al ser de arquitectura cerrada, no presentan la flexibilidad necesaria para su uso en la investigación. Para el caso de los modelos académicos analizados, que pueden ser de arquitectura abierta y brindar una mayor flexibilidad, aún no se encuentran en una etapa de desarrollo que brinde la confiabilidad necesaria para esta aplicación.
Objetivo General
Obtener un robot móvil volador autónomo (UAV) de dimensiones apropiadas para vuelos interiores a partir de componentes "off-the-shelf" capaz de realizar vuelo estático (hoovering) y desplazamientos con cambios de orientación y con los 3 grados de libertad estabilizados en intervalos cortos a partir de sensores inerciales on-board.
Objetivos Particulares
- Estudio de la dinámica de la estructura del robot. Definición de los parámetros constructivos principales y plantas propulsoras. Construcción del prototipo.
- Diseño y construcción del hardware para procesamiento de información obtenida de los sensores, control y drivers de potencia para motores.
- Cálculo, codificación y validación de la estrategia de control de la planta.
- Documentación del proyecto
Financiamiento
El financiamiento del proyecto es realizado por el Centro de Investigación de Informática para la Ingeniería como parte de un projecto de investigación.
Miembros del grupo de trabajo
Integrantes
Henze, Agustín Redolfi, Javier Andrés
Director:
Ing. David Gaydou, Ing. en Electrónica (UTN-FRC).
Organización del trabajo
El siguiente trabajo se organiza de la siguiente manera.
- En el capítulo 2 se explica el funcionamiento básico y el diseño del QA3.
- En el capítulo 3 se realiza el modelado de la planta, se diseña el controlador y se realizan las simulaciones correspondientes.
- El capítulo 4 nos presenta el filtro utilizado para realizar la medición de los ángulos de orientación de la aeronave.
- En el capítulo 5 se explican los diseños de los circuitos electrónicos y la construcción de las placas.
- En el capítulo 6 se comenta el software desarrollado y se explican sus partes fundamentales.
- En el capítulo 7 se realizan las conclusiones del trabajo realizado, junto con un análisis de costos.
Diseño del Cuadrotor
En esta sección se realiza una introducción al funcionamiento del Cuadrotor en general y se explica el diseño del QA3. En la sección del modelado matemático de la planta se amplía la información sobre el funciomiento.
El cuadricóptero, es una aeronave que se eleva y se desplaza por la acción cuatro rotores instalados al final de un marco en forma de cruz. El control se logra variando la velocidad angular de cada uno de los cuatro motores.
Introducción al Funcionamiento
Para controlar el QA3 es necesario generar cambios en la potencia entregada a cada motor. Para el siguiente análisis se asume que la plataforma esta volando estable con una potencia de motores PWMQ (en los cuatro motores).
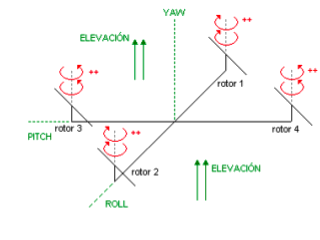
Los cuadricópteros como todo vehículo volador tiene 3 grados de libertad angulares, estos son roll, pitch y yaw.
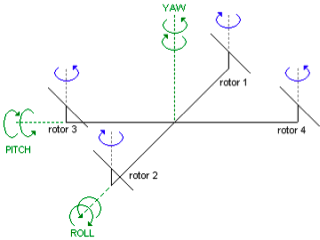
Movimiento de guiñada (yaw)
Se refiere al movimiento cuando el vehículo gira sobre su eje vertical. El cuadricóptero logra este movimiento aumentando (o disminuyendo) por igual la potencia de giro de los rotores 1 y 3 y disminuyendo (o aumentando) en igual magnitud los motores 2 y 4. Al disminuir esta potencia aumenta el par motor creando un giro contrario a las hélices que están rotando con mayor potencia. Las potencias de giro deben variar equilibradas para mantener el vehículo estacionario en el aire, es decir, la fuerza total constante.
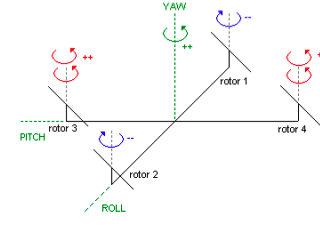
Movimiento de inclinación (pitch)
Es el movimiento que permite el movimiento hacia adelante y atrás. El vehículo mantiene la potencia en el rotor 1 que es opuesto al sentido deseado, reduce al mínimo la del rotor 3 y deja los otros dos a potencia media, así la sustentación del rotor 1 hace que el vehículo se incline a favor del sentido deseado y se desplace.
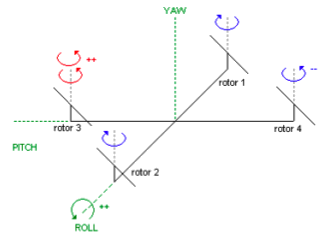
Movimiento de bamboleo (roll)
Es cuando el vehículo se mueve a la izquierda o derecha. Usa el mismo principio que el de inclinación, pero lateralmente. La combinación de los tres movimientos mencionados son los que hacen maniobrar al cuadricóptero libremente.
Los movimientos de roll y pitch son giros en torno a los ejes horizontales del QA3. Una inclinación en cualquiera de estos ejes produce un movimiento lineal en el plano horizontal cuya velocidad depende del ángulo (esto se denomina ángulo de ataque) y la dirección depende de la orientación del QA3. Yaw es un giro respecto a la vertical y no produce movimiento lineal.
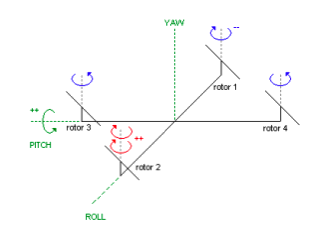
Movimiento Vertical
Por último, se puede hacer ascender, descender o mentener en vuelo estacionario al QA3, haciendo que la fuerza de sustentación generada por los 4 pares motores-hélices sea mayor que la fuerza peso generada por la atracción gravitatoria. Este movimiento se logra variando la potencia de los cuatro motores en igual medida para no modificar los demás grados de libertad. De esta forma la plataforma puede ascender o descender.
Lo dicho anteriormente es para el caso ideal, donde los cuatro motores tiene exactamente las mismas constantes y giran a las mismas velocidades angulares. En el caso real, lo anterior no es posible, porque siempre existen ciertas variaciones en las fuerzas generadas por los motores, ya sea por que las constantes de los motores son diferentes o las velocidades angulares giran a distintas revoluciones. Estas diferencias causarían que el vehículo tuviera ciertas rotaciones en su centro de gravedad y llevaría a que se la fuerza de sustentación total tuviera una diferencia angular con el eje Z. Esta diferencia daría lugar a un desplazamiento de en el plano XY.
El control de los movimientos yaw, pitch y roll se realiza con el sistema de navegación. En secciones siguientes se encontrarán las expresiones matemáticas que permitan modelar el comportamiento del cuadricóptero en el espacio. Los modelos matemáticos desarrollados serán simulados para luego ser probados en la estructura real.
Estructura
La estructura del QA3 es de aluminio compuesta por dos tubos rectangulares (2mm de espesor, 60cm de largo) encastrados en sus centros, formando un ángulo de 90º. Sobre el centro se encuentra la placa madre montada sobre gomas de caucho para amortiguar las vibraciones producidas por los motores.
Como se observa en la figura anterior, se realizaron ventanas sobre los tubos para no obstaculizar el flujo de aire generado por las hélices. Con esto se logra un aumento en el empuje generado por los propulsores.
Cálculo del peso total
En la siguiente tabla se especifican los pesos de los componentes utilizados, algunos fueron obtenidos del fabricante y otros a través de mediciones.
Motores |
4 |
52g |
208g |
ESC |
4 |
32g |
128g |
Baterías |
2 |
160g |
320g |
Hélices |
4 |
10g |
40g |
Estructura |
1 |
300g |
300g |
Protección |
1 |
150g |
150g |
Placa Madre |
1 |
200g |
200g |
Montaje Placa |
1 |
150g |
150g |
Total |
1496g |
||
Con el pesaje del prototipo completo con una balanza de presición se obtuvo un valor de 1482g, el cual es muy cercano al valor calculado anteriormente.
Motores
Se utiliza motores brushless para aeromodelismo con control electrónico. A diferencia de un motor DC convencional, en un motor brushless la armadura no tiene movimiento y el imán permanente es el que gira sobre su eje. Estos motores son conocidos como outrunners. Para lograr esto es necesario generar tres señales con valor eficaz variable en forma cuasi-senoidal, como se muestra en el siguiente gráfico.
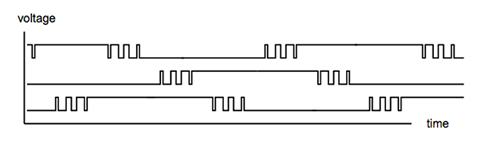
Un parámetro importante de éste tipo de motores es el
, constante que relaciona la velocidad en RPM del motor sin carga con el valor pico de tensión en las bobinas del motor. Los motores elegidos son los BL-2830-8 de la empresa RCTimer que tienen un
.

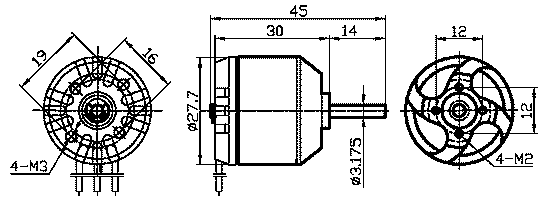
Las características de estos motores son:
- Modelo: 2830-8
- Dimensiones: Ф28*30mm
- Dimensión del eje: Ф3.17*45mm
- Peso: 52g
- KV(rpm/V): 1300
- Potencia Máxima: 275W
- Batería: 2-4Li-Po
- Hélices recomendadas: 9x6/7x3
- Ri(M Ω): 0.075
- ESC(A): 30A
Controladores ESC
Los controladores de los motores (ESC, Electronic Speed Controller) permiten regular la potencia suministrada a cada motor. Se alimentan con una tensión formada con celdas NiMh o LiPo. En nuestro caso la tensión es 12v. La salida del ESC debe ser como la mostrada en la figura anterior.
En un primer momento se planeo la construcción de un controlador de velocidad, pero debido a varias razones se decidió la compra de un ESC comercial. La principal razón de esta decisión fue el costo de la construcción de un ESC. El precio de un controlador comercial esta en el orden de los 200. Las razones de este costo elevado son la necesidad de usar transistores mosfet especiales que no se consiguen facilmente, los transistores deben manejar 30A de corriente continua y picos de 100A, también deben tener tensiones de disparo bajas compatibles con las de un microcontrolador para no complicar el circuito. También se necesita contar un microcontrolador con 6 salidas de PWM, lo que no es muy común en los microcontroladores normalmente usados.
Si agregamos a todo esto el tiempo de desarrollo y de prueba, llegamos a la conclusión de que carece de sentido construir el controlador en el ámbito de nuestro proyecto.
En la sección de hardware se amplía la información sobre los controladores comerciales usados.
Baterías LiPo
Actualmente las baterías de Litio-Polímero son usadas para este tipo de aplicaciones en donde se necesitan elevadas potencias y bajo peso. Estas baterías están formadas por celdas que se pueden agrupar en serie y paralelo para lograr los voltajes y corrientes necesarios.
Las baterías LiPo necesitan cargadores especiales. Sus celdas no deben ser sobrecargadas ni tampoco deben ser descargadas profundamente. Para mantener la diferencia entre las celdas al mínimo, se debe usar un balanceador. Este balanceador puede estar integrado al cargador o puede estar separado. Por esto las baterías no solamente tienen los bornes normales de una batería, sino que tienen otro conector que nos permite acceder a las celdas individuales para lograr una carga balanceada.
El manejo de estas baterías debe ser realizado con precaución, por lo tanto se deben tener en cuenta algunas reglas. El fabricante nos aconseja:
- No exceder de 4.2V el voltaje de cada celda.
- No exceder de 5C la tasa de carga
- No exceder las tasas de descarga de corrientes especificadas
- No descargar la batería a más de menos de entre un 10 a 20% de su capacidad energética. Usar 3.4V como tensión de corte de celda.
- Siempre monitorear la carga de la batería
- Nunca cortocircuitar, tampoco exponer al fuego o al agua
- Nunca usar un pack estropeado
Se planteó el diseño del prototipo con una autonomía de vuelo de aproximadamente 10 minutos. El QA3 posee 2 baterias Hyperion G3 CX - 3S 2100mAh (25C).
Cálculo de la autonomía de vuelo
Se realizará un cálculo aproximado de este tiempo debido a que el mismo depende de los tipos de maniobras que realiza el dispositivo.
Primero vamos a suponer que trabajamos a potencia máxima:
4 Motores de 275W = 1100W Potencia total consumida, despreciando el resto de los componentes.
2 Baterías de 11.1V * 2100mAh = 46.62Wh
Este tiempo está calculado a potencia máxima, como vemos el QA3 sin llevar carga y volando manteniéndose estático en un punto reduce esta energía consumida a aproximadamente un 25%.

Características:
- Peso: 160g
- Dimensiones: 109 x 36 x 24 mm
- Tecnología Lipo
- Velocidad de carga de hasta 5C
Hélices
Para el funcionamiento del QA3 se necesitan que 2 hélices giren en un sentido y las otras 2 en otro sentido, esto hace que si la sumatoria de las 2 velocidades de las que giran en un sentido es igual a la sumatoria de las que lo hacen en sentido contrario contrario, el torque resultante se cancela.
Las hélices más comunes son las que se usan en el morro del avión, están son conocidas como hélices normales. Hay otro tipo de hélices llamadas empujadoras o pusher en inglés que son las que se utilizan en aeronaves que tienen generan su empuje en la cola. Una posible solución a este problema sería girar 180º la hélice sobre su eje y colocarla en el motor. Pero esta solución tiene corto alcance debido a que el empuje generado por la misma hélice cuando gira en su sentido normal es distinto al generado cuando gira en el otro sentido.
Las hélices empujadoras están diseñadas para que el empuje generado por su rotación sea más efectivo cuando giran al revés que una hélice normal.
Las hélices en general tienen 2 parámetros que las caracterizan: el paso y el diámetro.
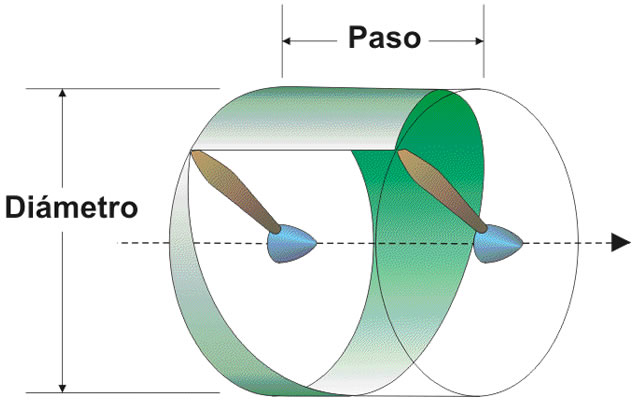
El paso se calcula como la distancia que recorrería la hélice en una vuelta si esta se moviese en un medio sólido (semejante a un tornillo) y el diámetro es el del círculo que generan cuando estás rotan. Este diámetro me indica el área del aire que entra en juego en el cálculo del empuje.
Las hélices definen el consumo de corriente de los motores, así como el empuje que se puede lograr.
Las hélices utilizadas en el QA3 son las recomendadas por el motor, con una medida de 9x6 pulgadas.


Protección
Para poder realizar pruebas seguras con el QA3 y evitar que el proyecto dure más que un solo vuelo, se decidió armar una estructura de telgopor, de manera que las hélices queden contenidas dentro del volumen formado. También se le añadió unos pies para proteger el conexionado de alimentación. Estos pies también permiten calibrar el "cero" fácilmente.
Modelado del Quadrotor
En este capítulo se realiza la derivación del modelo matemético de la planta del QA3, también se realizan las simplificaciones necesarias para poder obtener un controlador simple, pero con una buena performance, luego se explican las mediciones realizadas para obtener las constantes reales de la planta y aplicarlas al modelo. Por último se diseña el controlador.
La derivación de la dinámica no lineal es realizada en coordenadas inerciales NED y de cuerpo fijo. Denotemos con {
,
,
} los ejes inerciales, y con {
,
,
} a los ejes del cuerpo. Los ángulos de Euler de los ejes del cuerpo son {
,
,
} con respecto a los ejes
,
y
respectivamente, y son referidos como roll, pitch and yaw. Definamos a r como el vector de posición desde el origen inercial hacía el centro de gravedad del vehículo(CG), y dejemos que
sea definido como la velocidad angular en con respecto al eje de referencia del cuerpo.
La dirección actual de la velocidad es referida como
en coordenadas inerciales. Los rotores, numerados 1-4, están montados sobre los ejes
,
,
y
, respectivamente, con vectores de posición
con respecto a CG. Cada rotor produce un torque aerodinámico
y un empuje
, ambos paralelos al eje de rotación del rotor, y ambos usados para el control del vehículo.
Aquí,
, donde
es el voltage aplicado a los motores. En vuelo,
puede variar mucho con respecto a esta aproximación. Los torques,
, son proporcionales al empuje del rotor y están dados por
.
Los rotores 1 y 3 giran en dirección opuesta a los rotores 2 y 4, por esto los torques aerodinámicos se contrarrestran y pueden ser usados independientemente para el control de yaw. La velocidad horizontal resulta en un momento en los rotores,
, sobre
, y una fuerza de arrastre,
, en la dirección
. La fuerza de arrastre de cuerpo está definida como
, la masa del vehículo es
, la aceleración debido a la gravedad es
, y la matriz de inercia es
. Un diagrama de cuerpo libre se muestra en la figura siguiente.
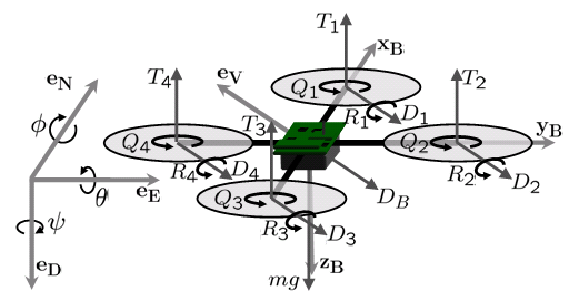
La fuerza total,
, y el momento,
, puede ser sumado como
La dinámica no lineal completa puede ser expresada como:
donde se asume que el momento angular total de los rotores está cerca de cero, porque están en contra rotación.
Descripción
Fuerza de Arrastre del Cuerpo
Empuje
Fuerza de arrastre sobre los rotores debido a la velocidad horizontal
Momento de arrastre sobre el eje de rotación de los rotores
Momento de Roll generado en los rotores por la velocidad
Fuerza de arrastre en los rotores debido a la velocidad
Empuje Total
Aproximación de la Fuerza y el Momento
Suponiendo que el Cuadricóptero está en vuelo estacionario podemos despreciar
y
. Con esto nos queda:
Fuerza
Aproximando las matrices de rotación de los ángulos para ángulos pequeños, tenemos:
Momento
También podemos despreciar los momemtos de Rolling
y
. El Torque nos queda:
Referencias
[[ http://www.eecs.berkeley.edu/~tomlin/papers/conferences/whjt05_iros.pdf | Multi-Agent Quadrotor Testbed Control Design: Integral Sliding Mode vs. Reinforcement Learning ]]
Path Tracking Control for Quadrotor Helicopters
Medición de los parámetros de la Planta
Para el diseño del controlador del quadricóptero resulta necesario realizar la medición de los distintos parámetros del modelo real. Los parámetros fundamentales son el peso, el momento de inercia, los empujes de los motores.
Empuje de los motores
Al momento de realizar esta medición poseíamos 2 motores rctimer 2830, 1 ESC rctimer de 30A, 1 ESC mystery de 30A, 1 hélice con paso normal y una hélice con paso pusher.
Se realizó la medición del empuje de cada motor, con las distintas hélices y los dos controladores. Esta medición se hizo montando el motor sobre un peso de plomo, el cual se ponía sobre la balanza y luego se realizaron las curvas de transferencia entre PWM y fuerza de empuje. El montaje se muestra en la siguiente figura.

En las siguientes tablas se muestran los resultados obtenidos, RCTimer y Mystery son los 2 controladores usados, Normal y Pusher son los 2 tipos de hélices. También se muestran los datos en forma gráfica.
Como se puede ver, podemos aproximar la función de transferencia entre el ciclo de trabajo y el empuje generado por una recta. Esta es una aproximación no tan real debido a que se desprecian todas las constantes de tiempo del motor y de la hélice. Obtener una función de transferencia real para el conjunto motor hélice representa un trabajo que sobrepasa nuestros conocimientos y objetivos, por lo tanto en adelante se supondrá que la transferencia entre ciclo de trabajo y empuje es una constante.
Motor 1
RCTimer Normal
Duty |
2949 |
5898 |
8847 |
11796 |
14745 |
17694 |
20643 |
23592 |
26541 |
29491 |
32440 |
35389 |
38338 |
41287 |
Fuerza |
0 |
55 |
100 |
145 |
185 |
230 |
270 |
320 |
360 |
400 |
440 |
490 |
540 |
600 |
Mystery Pusher
Duty |
2949 |
5898 |
8847 |
11796 |
14745 |
17694 |
20643 |
23592 |
26541 |
29491 |
32440 |
35389 |
38338 |
41287 |
Fuerza |
20 |
20 |
95 |
165 |
245 |
325 |
410 |
480 |
575 |
670 |
770 |
855 |
855 |
845 |
RCTimer Pusher
Duty |
2949 |
5898 |
8847 |
11796 |
14745 |
17694 |
20643 |
23592 |
26541 |
29491 |
32440 |
35389 |
38338 |
41287 |
Fuerza |
5 |
60 |
105 |
150 |
195 |
240 |
290 |
335 |
380 |
425 |
475 |
540 |
605 |
665 |
Mystery Normal
Duty |
2949 |
5898 |
8847 |
11796 |
14745 |
17694 |
20643 |
23592 |
26541 |
29491 |
32440 |
35389 |
38338 |
41287 |
Fuerza |
5 |
5 |
80 |
150 |
225 |
300 |
380 |
460 |
545 |
640 |
730 |
790 |
760 |
760 |
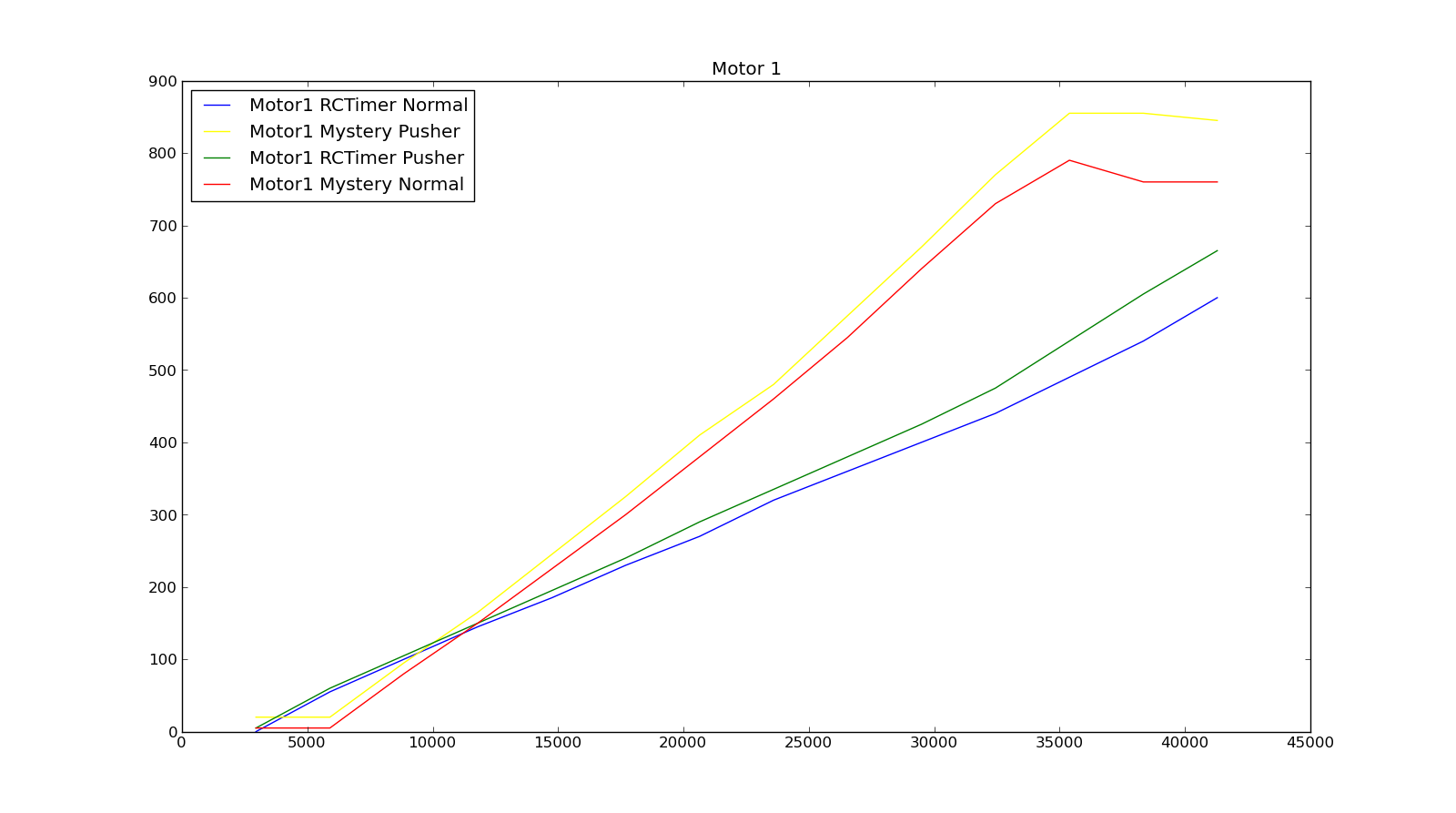
Motor 2
Mystery Normal
Duty |
2949 |
5898 |
8847 |
11796 |
14745 |
17694 |
20643 |
23592 |
26541 |
29491 |
32440 |
35389 |
38338 |
Fuerza |
15 |
15 |
80 |
160 |
235 |
320 |
395 |
475 |
570 |
665 |
765 |
840 |
840 |
RCTimer Pusher
Duty |
2949 |
5898 |
8847 |
11796 |
14745 |
17694 |
20643 |
23592 |
26541 |
29491 |
32440 |
35389 |
38338 |
41287 |
Fuerza |
10 |
65 |
110 |
155 |
200 |
245 |
295 |
345 |
395 |
435 |
490 |
560 |
605 |
660 |
Mystery Pusher
Duty |
2949 |
5898 |
8847 |
11796 |
14745 |
17694 |
20643 |
23592 |
26541 |
29491 |
32440 |
35389 |
38338 |
Fuerza |
5 |
5 |
80 |
155 |
245 |
335 |
425 |
535 |
655 |
795 |
905 |
1015 |
1015 |
RCTimer Normal
Duty |
2949 |
5898 |
8847 |
11796 |
14745 |
17694 |
20643 |
23592 |
26541 |
29491 |
32440 |
35389 |
38338 |
41287 |
Fuerza |
25 |
65 |
110 |
155 |
195 |
235 |
275 |
315 |
360 |
400 |
435 |
485 |
540 |
595 |
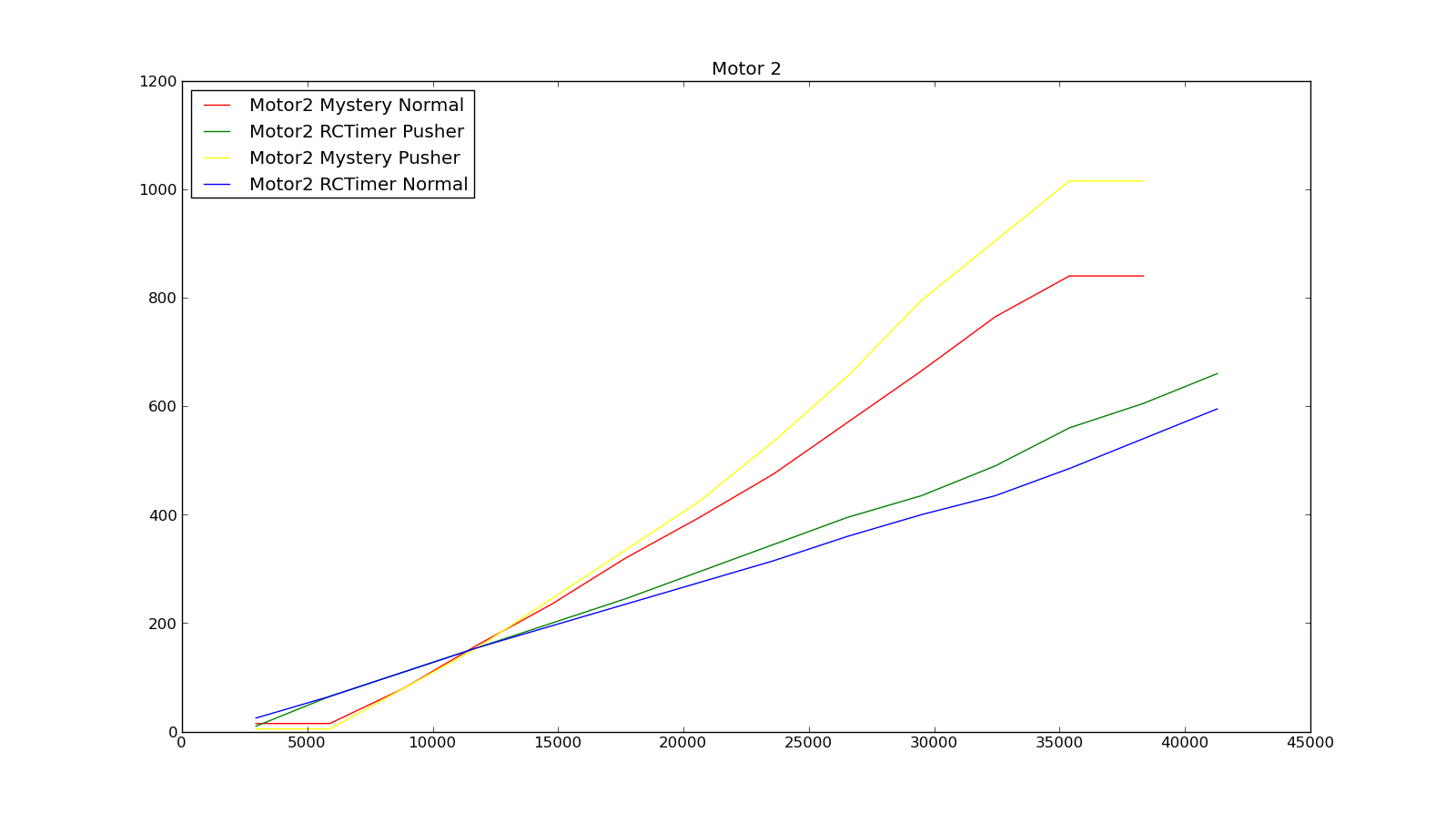
Motor1, RCTimer, Pusher y Motor2, Mystery y Normal
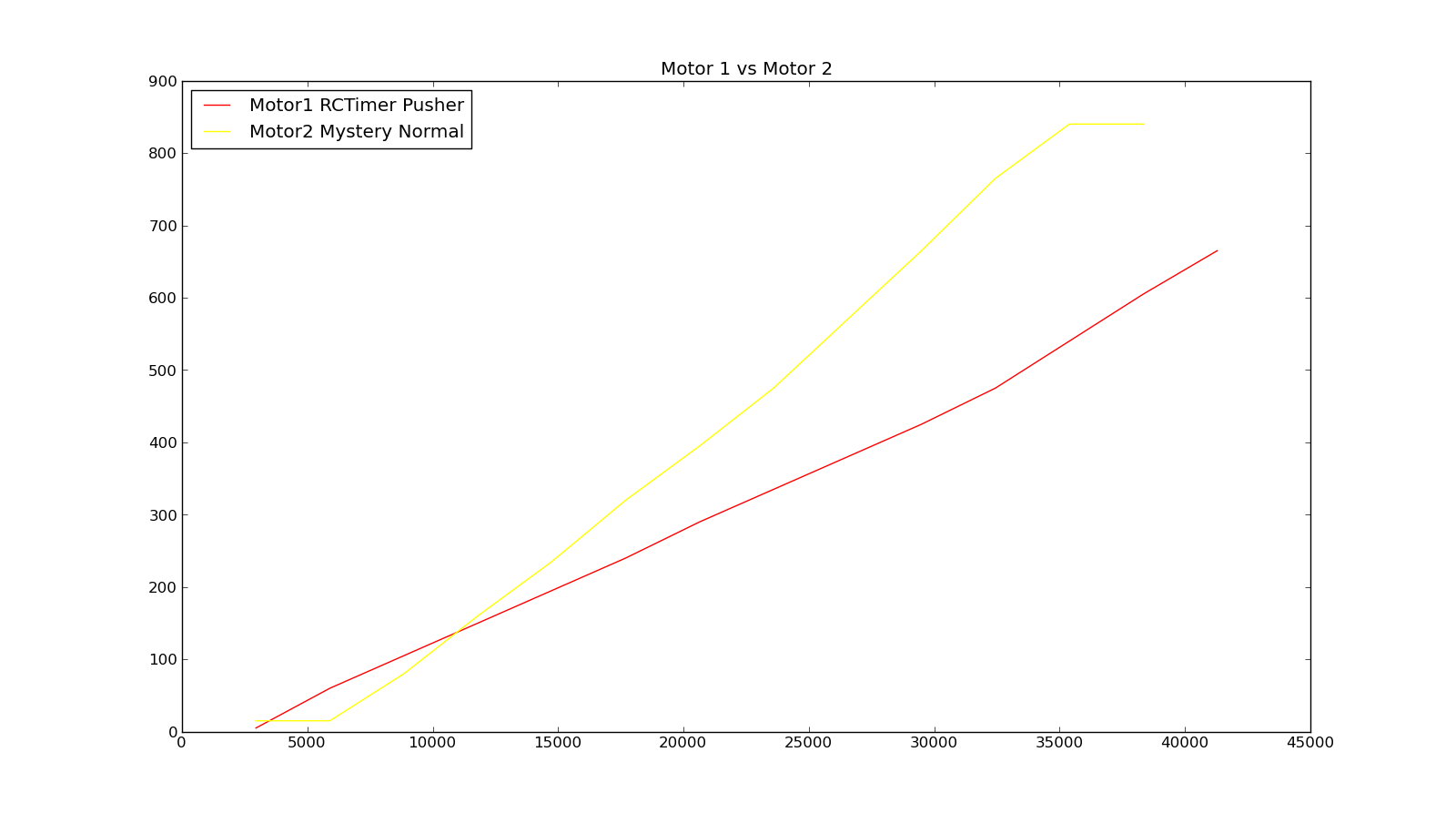
Cálculo Aproximado de las constantes
Cálculo de la constante de Inercia
Cálculo de la constante del Motor
Según las mediciones realizadas podemos aproximar estas constantes.
Revisión del Cálculo de las constantes
Esta revisión se hace para adaptarla al nuevo modelo del QA3, que tiene 1 metro de largo en las barras y usa la imu 3DM-GX1.
Partes: las partes que vamos a usar para calcular el momento de inercia son el motor, las baterías, las barras, la IMU y la placa del ARM.
Inercias con respecto al eje X o Y
Motor
Para calcularlo suponemos que el motor es un cilindro
donde m es la masa total del motor y r es el radio del motor.
Usando el teorema de Steiner nos queda:
donde d es la distancia del motor al centro de gravedad, en este caso la mitad del largo de la barra.
Batería
Para calcularlo suponemos que la batería es un paralelepípedo rectangular.
En donde b y c son los lados del paralelepípedo perpendiculares al eje con respecto al que calculamos el momento de inercia.
En nuestro caso
y
Otra vez por el teorema de Steiner nos queda que:
en donde d representa la distancia del CG a la batería,
Barra
Supondremos que la barra es una línea perpendicular al eje sobre el que calculamos el momento de inercia. La masa de las barra es
y
es el largo total de la barra.
El peso de la barra sin fresar es de
. El peso de las 2 barras fresadas es de
.
IMU, ARM
Supondremos que la placa central es un cubo de lado
y masa
.
Momento total de inercia para el eje x o y
Diseño del controlador
El problema del diseño de un controlador de actitud para el QA3 no es un problema trivial debido a varias razones como son el acoplamiento entre las fuerzas y momentos generados por los motores y hélices, el rozamiento con el aire, la fuerza de empuje del viento, etc; por esto se ha optado por el uso de un controlador PID, el cual se puede ajustar para las mejores condiciones de funcionamiento y de la realización de varias simplificaciones.
La primera simplificación importante es suponer que el control de los distintos ángulos esta desacoplado. Con esta suposición obtenemos 3 plantas independientes a las cuales les agregamos un controlador PID distinto.
Otra simplificación es suponer que las fuerzas de rozamiento con el aire y la fuerza generada por corrientes de aire son despreciables. Estas corrientes de aire no solo se pueden deber al viento, sino también a rebotes del flujo de aire generado por la hélice con el entorno.
También despreciamos la dinámica del motor y suponemos que es lineal.
En esta sección se explica el controlador PID y los 3 controladores de los ángulos.
Controlador PID
Un controlador PID (Proporcional Integral Derivativo) es un mecanismo de control por realimentación que calcula la desviación o error entre un valor medido y el valor que se quiere obtener, para aplicar una acción correctora que ajuste el proceso.
El algoritmo de cálculo del control PID tiene tres parámetros distintos: el proporcional, el integral, y el derivativo. El valor Proporcional determina la reacción del error actual. El Integral genera una corrección proporcional a la integral del error, esto nos asegura que aplicando un esfuerzo de control suficiente, el error de seguimiento se reduce a cero. El Derivativo determina la reacción del tiempo en el que el error se produce. La suma de estas tres acciones es usada para ajustar al proceso vía un elemento de control, en este caso el PWM aplicado a los motores. Ajustando estas tres variables en el algoritmo de control del PID, el controlador puede proveer un control diseñado para lo que requiera el proceso a realizar.
La respuesta del controlador puede ser descrita en términos de respuesta del control ante un error, el grado el cual el controlador llega al "set point", y el grado de oscilación del sistema. Nótese que el uso del PID para control no garantiza control óptimo del sistema o la estabilidad del mismo. Algunas aplicaciones pueden solo requerir de uno o dos modos de los que provee este sistema de control.
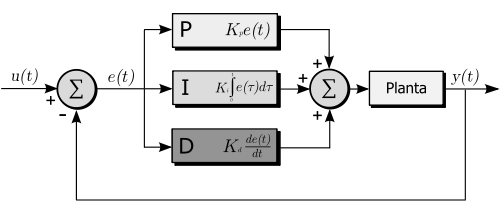
Ecuacion Diferencial
La ecuación diferencial de un controlador PID tiene la siguiente forma:
Transformada de Laplace
Aplicando la transformada de Laplace a la ecuanción diferencial anterior podemos encontrar la relación entre entrada y salida en el plano de Laplace:
Transformada Z
Para realizar el análisis en tiempo discreto necesitamos pasar del plano de Laplace al plano Z. Esto se hace aplicando la transformada Z a la función obtenida anteriormente. Una vez obtenida la función en el plano Z, podemos realizar análisis de estabilidad, de respuesta y realizar el controlador para obtener la respuesta deseada.
a
Podemos definir 3 constantes,
,
,
, y expresar la ecuación anterior como:
Está última forma tiene una similitud con el controlador PID en tiempo continuo, pero aclaramos que las constantes no son las mismas.
Tiempo Discreto
Para poder codificar el algoritmo en un microcontrolador, debemos pasar la función de transferencia en el plano Z, a una ecuación en diferencias en el tiempo. En la ecuación siguiente se muestra el algoritmo del controlador PID en el tiempo.
A continuación se realiza el análisis de los controladores de los ángulos de roll y pitch.
Controlador del ángulo de roll
El ángulo de roll depende de la diferencia del empuje entre los motores laterales. A continuación se realiza el cálculo de la función de transferencia a lazo cerrado de la planta más el controlador PID. Suponemos primero un modelo continuo y luego un modelo discreto con un retenedor de orden cero, para tener en cuenta el retardo de fase introducido por el muestreo.
Modelo Continuo
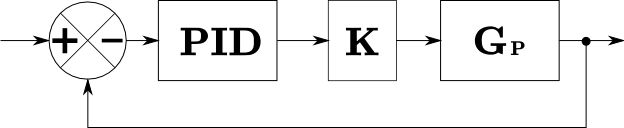
Modelo Discreto

Controlador del ángulo de pitch
El ángulo de pitch depende de la diferencia del empuje entre los motores delantero y trasero. El controlador de este ángulo es igual al del controlador del roll, por esto no nos extendemos en este controlador.
Simulaciones
Para las simulaciones se van a utilizar las ecuaciones obtenidas anteriormente de la planta más el controlador. Estas fueron realizadas con el software octave.
Los valores de los parámetros usados fueron extraídos del modelo real y son los siguientes.
Simulación a lazo abierto
Se muestran los resultados de la simulación de la planta más el controlador diseñado en lazo abierto. Con estos datos podemos saber como será la respuesta del sistema según el valor de k elegido. Como se puede observar para valores de k muy grandes el sistema se vuelve inestable.
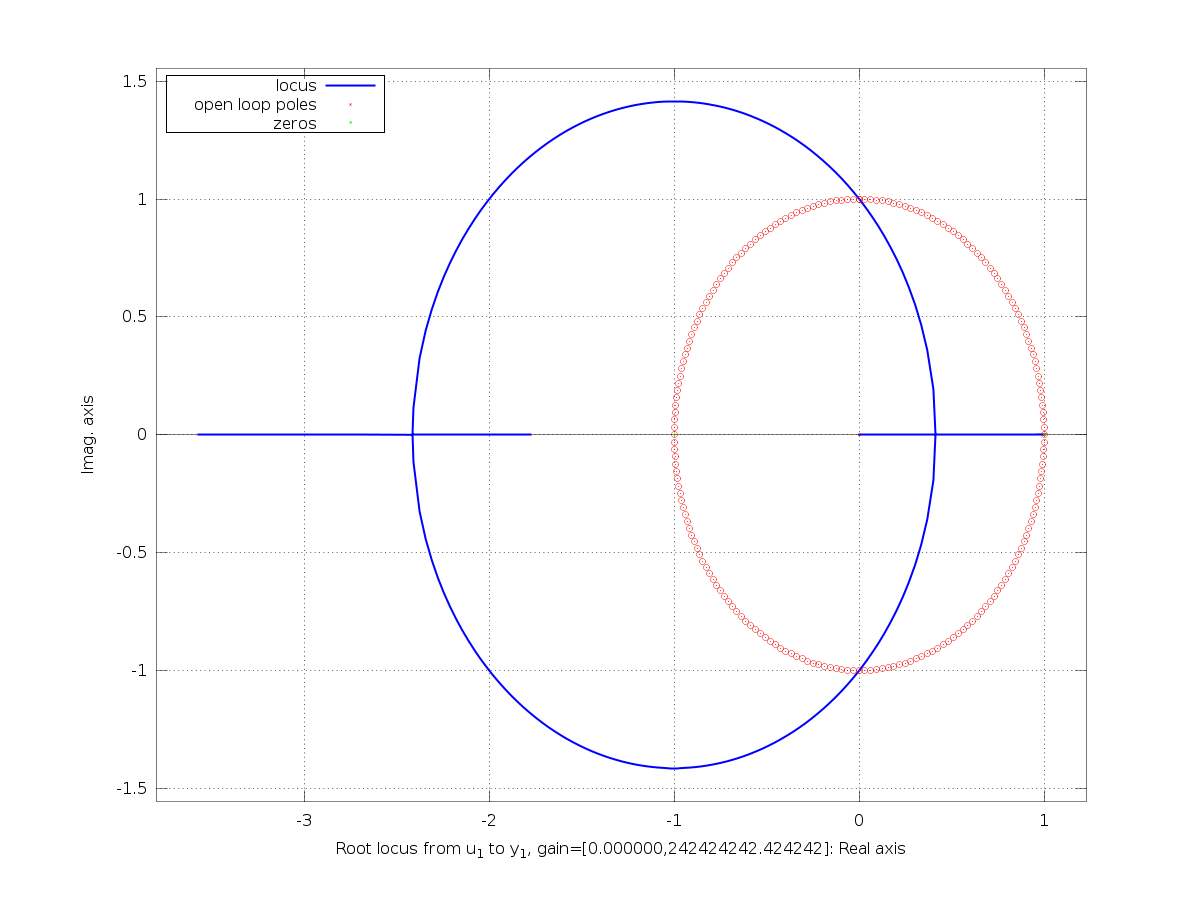
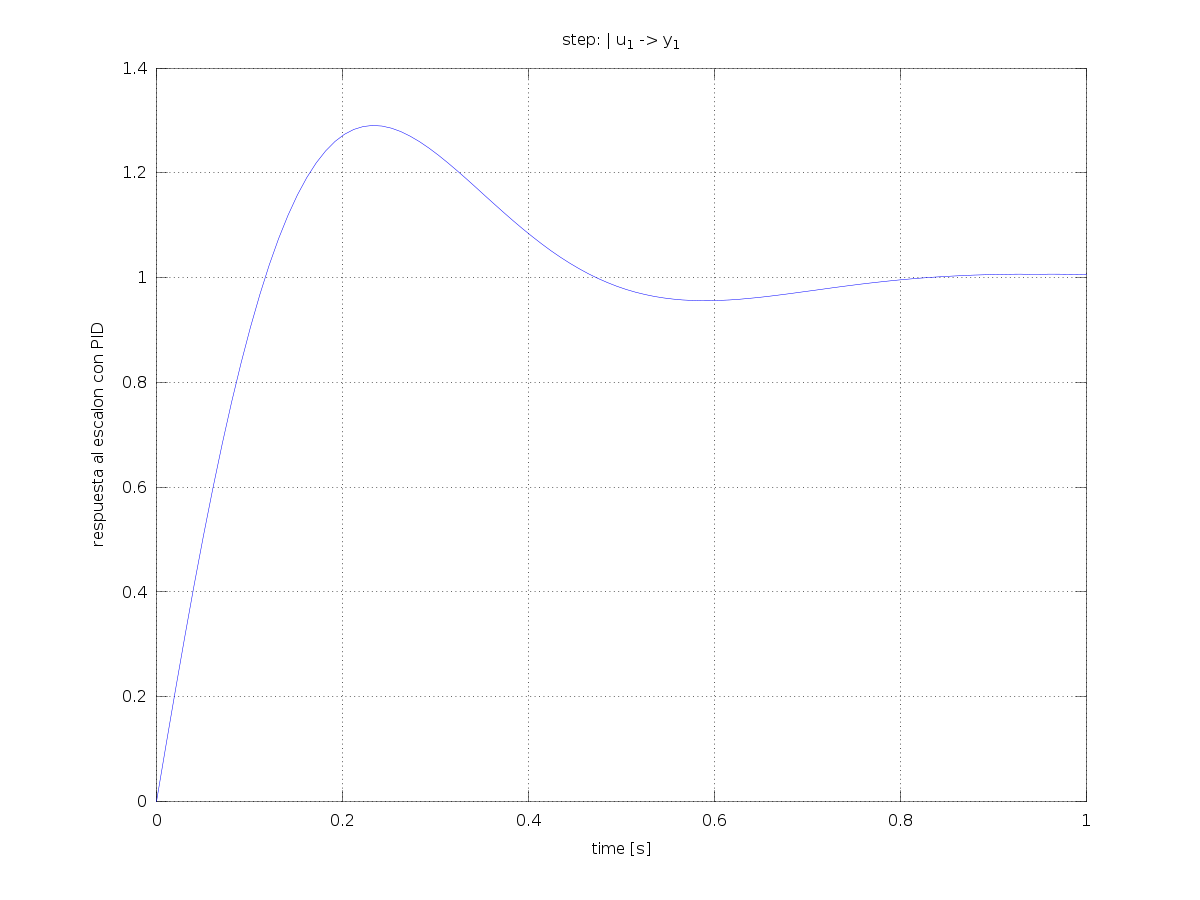
Simulación a lazo cerrado
En esta simulación se muestran los resultados de la simulación de la salida en función del tiempo para una entrada escalón.
Filtro Complementario para la Estimación del ángulo de roll y de pitch
En este capítulo se presenta un sistema para estimación de actitud del QA3. Para determinar la inclinación se utilizan acelerómetros tipo MEMS, que poseen numerosas ventajas para esta aplicación, como ser buen ancho de banda, suficiente resolución, peso reducido, robustez y bajo costo. Mediante estos sensores es posible determinar la dirección y el sentido del vector de aceleración de la gravedad respecto a un marco de referencia fijo en la aeronave. La desventaja fundamental de estos sensores radica en que las mediciones son fuertemente afectadas por las vibraciones en la estructura donde se encuentran montados.
Otra alternativa para medir la inclinación es computar la rotación integrando la señal de sensores giroscópicos. Por las mismas razones que el caso anterior, los dispositivos de tecnología MEMS resultan los más apropiados para esta aplicación, aunque si bien son más inmunes a las vibraciones presentan derivas sostenidas en el tiempo debido a la integración de los errores de offset.

Ensayo individual de los sensores
Para los ensayos que se describen a continuación se construyó un montaje experimental que consta de un balancín con un propulsor en cada extremo, un potenciómetro en el pivot y el sensor con el sistema de control montado en el centro. Este montaje con un grado de libertad permite simular el comportamiento dinámico aproximado del sistema respecto al rolido o el cabeceo. Aparte del sistema mecánico, el montaje cuenta con un controlador PID digital implementado en el microcontrolador, el cual cierra el lazo del sistema a través del control de la velocidad de los motores. Para lograr una notación consistente supondremos que el ángulo a medir es el de rolido (
).
Acelerómetro
En el desarrollo experimental se utilizó el acelerómetro ADXL345 de tres ejes dispuesto de manera que los ejes de medición del mismo coincidan con los ejes del sistema de referencia del UAV. De esta manera el ángulo se obtiene como:
,
donde la aceleración
se mide con una resolución de 10 bits, y un ancho de banda ajustable por software desde 0.05 Hz. hasta 1600 Hz.
Las siguientes muestran comparativamente las señales adquiridas del sistema a lazo abierto en estado de equilibrio con una inclinación de 10º con los propulsores apagados y con los propulsores encendidos (50\%) respectivamente.
Angulo medido con el giroscopio, con el montaje en equilibrio y los propulsores apagados.
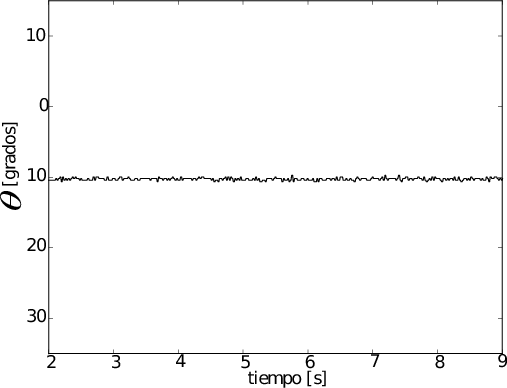
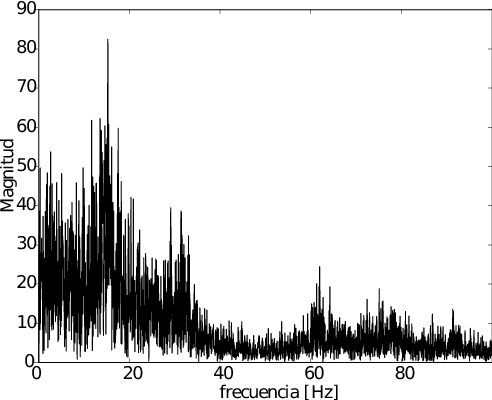
Ángulo medido con el acelerómetro, con el montaje en equilibrio formando un ángulo de 10º y los propulsores encendidos al 50% de su potencia:
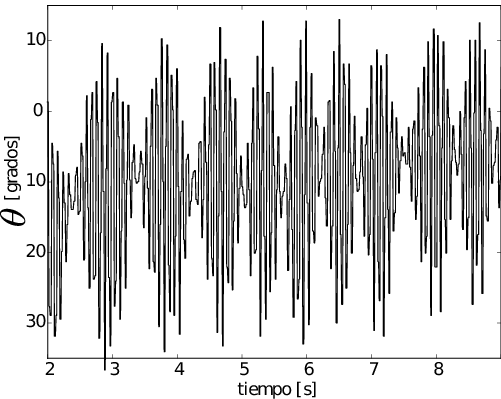
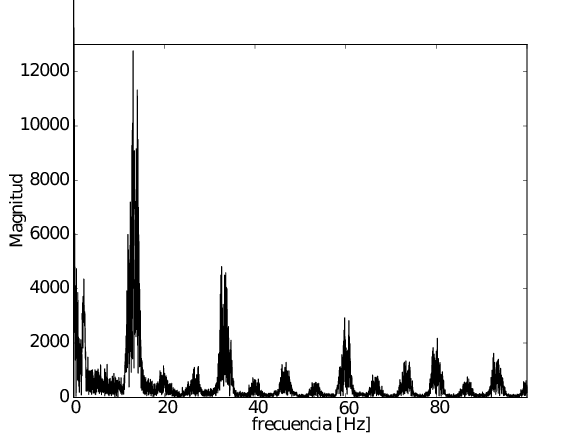
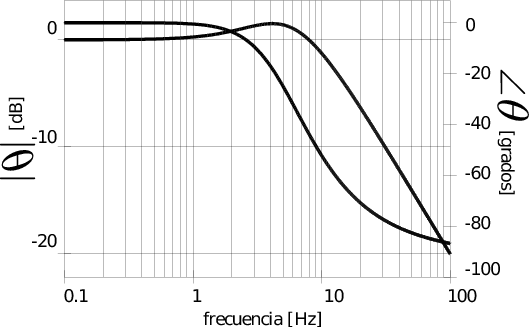
Respuesta en frecuencia del sistema completo a lazo cerrado:
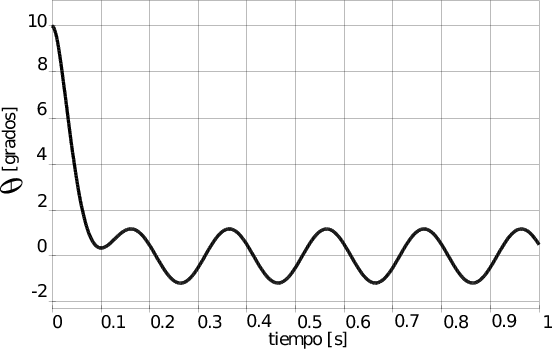
Respuesta temporal del sistema de lazo cerrado de tipo regulador con una perturbación sumada a la medición ideal de de amplitud para frecuencias de 5Hz y 50Hz:
Frecuencia de la perturación de 5Hz:
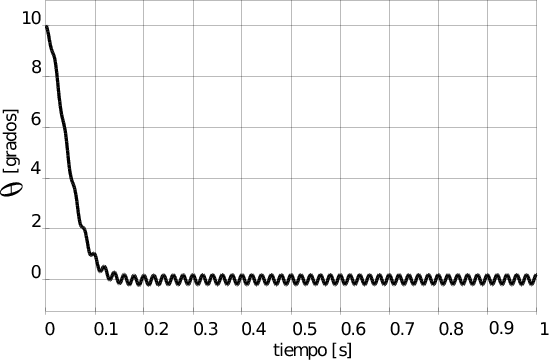
Frecuencia de la perturación de 50Hz:
Respuestas temporales del sistema a lazo cerrado de para señales no ruidosas, pero previamente pasadas por un filtro pasa bajos:
Sin filtrar:
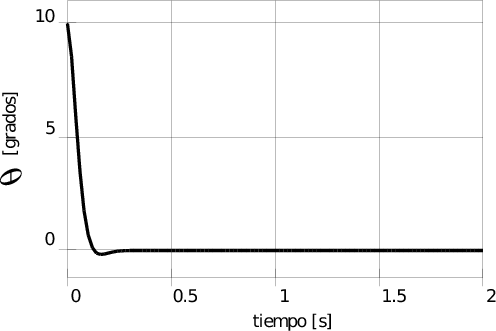
:
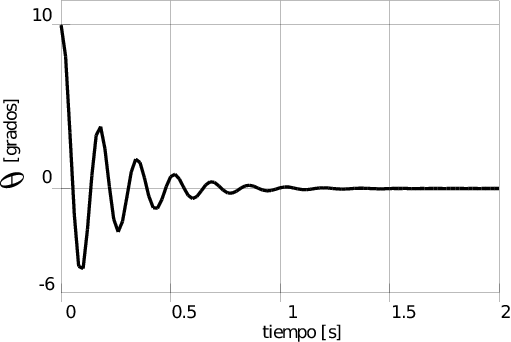
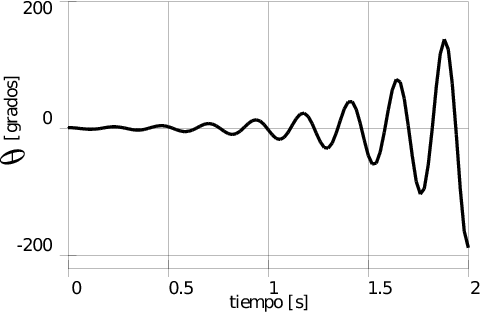
Si bien el sistema en lazo cerrado formado por el balancín más el controlador PID presenta un buen rechazo a las componentes ruidosas de alta frecuencia de las vibraciones, esto se aprecia en la curva de bode simulada para un sistema ideal y en las curvas de respuesta en el tiempo del mismo sistema que se ven en las figuras anteriores, las variaciones bruscas de la señal de referencia producen acciones de control, debidas a la rama del derivador del compensador, que llevan a los motores a zonas no lineales (saturación o corte), provocando la inestabilidad del sistema real.
El filtrado de la señal ruidosa mediante un filtro pasa-bajos introduce otras desventajas: si bien se pueden mantener acotadas las derivadas en la señal, la atenuación y el corrimiento de fase degradan la respuesta dinámica e incluso provocan inestabilidad cuando las frecuencias de corte son demasiado bajas. En las imágenes anteriores también se muestra la respuesta temporal del sistema para una medición no ruidosa y no filtrada, y la respuesta cuando la misma señal se pasa por un filtro pasa-bajos de 5 Hz de frecuencia de corte, finalmente si se disminuye la frecuencia de corte del mismo a 2 Hz el sistema se desestabiliza, tal como lo muestra la última gráfica.
Como consecuencia de las características ruidosas de las mediciones adquiridas con el acelerómetro no sería posible utilizarlo como inclinómetro en el sistema de estabilización. A raíz de esto se evalúa la posibilidad de utilizar un giróscopo.
Giróscopo
Para realizar los siguientes experimentos se utilizó un giróscopo de 3 ejes ITG-3200 de la firma InvenSense. Éste se dispuso de manera que sus ejes estén alineados con los del sistema de referencia de a bordo. Este dispositivo posee un rango dinámico de
y una sensibilidad de
. En las siguientes se observan comparativamente las señales en el tiempo y el espectro para el caso que los propulsores están apagados y encendidos con la misma configuración que la descripta para el caso de la medición con el acelerómetro. Haciendo una comparación de las figuras se puede ver que la influencia de las vibraciones en las mediciones del giróscopo son sensiblemente menores que en el caso del acelerómetro. Sin embargo se han observado intérvalos de tiempo relativamente cortos. También se muestra que para tiempos mayores la medida de este sensor comienza a derivar.
Ángulo medido con el giroscopio, con el montaje en equilibrio y los propulsores apagados:
Ángulo de rolido en función del tiempo:
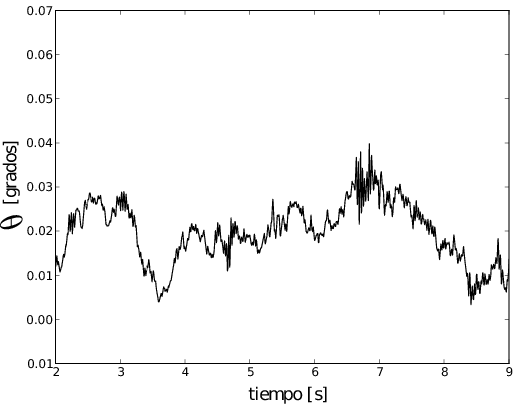
Espectro de frecuencias:
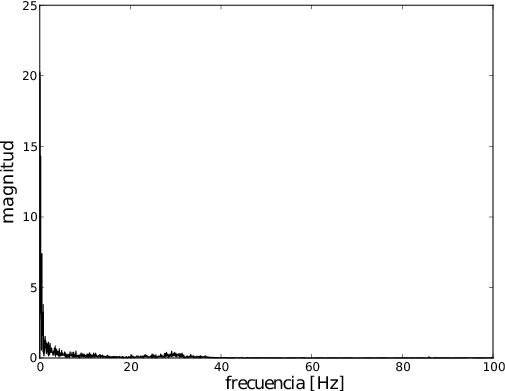
Ángulo medido con el giroscopio, con el montaje en equilibrio y los propulsores encendidos al 50\% de su potencia:
Ángulo de rolido en función del tiempo:
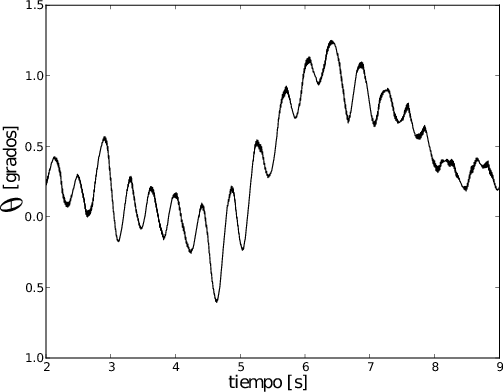
Espectro de frecuencias:
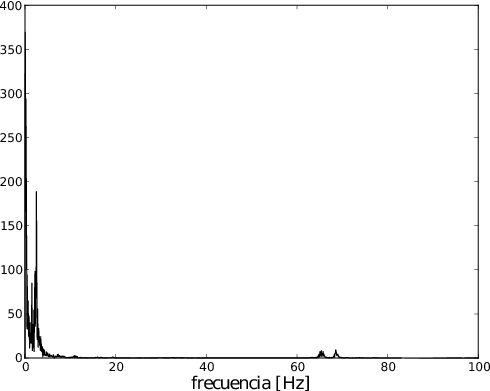
Deriva del ángulo medido por el giróscopo:

Filtro Complementario
En forma intuitiva surge la idea de usar la medición obtenida por el giróscopo para tiempos cortos y realizar la corrección de la deriva con la medición realizada por el acelerómetro en tiempos largos, debido a que esta última medición tiende a ser la aceleración de la gravedad para períodos largos.
Los filtros complementarios son muy usados en sistemas de navegación inercial. Aplicaciones típicas son la combinación de las medidas de aceleración vertical y velocidad barométrica vertical para obtener una estimación de la velocidad vertical o mediciones de unidades inerciales y sistemas de visión. \cite{buskey2004helicopter}
Un filtro complementario es en sí un filtro de Kalman de estado estacionario para una cierta clase de problemas de filtrado \cite{higgins2007comparison}, este no considera ninguna descripción estadística del ruido que corrompe a las señales y es obtenido solamente por un análisis en el dominio de la frecuencia.
El filtro complementario resulta sencillo de tratar matemáticamente y en razón de su baja complejidad de implementación consume pocos recursos computacionales.
La idea básica del filtro complementario es combinar la salida del acelerómetro y del giróscopo para obtener una buena estimación del ángulo de orientación de la plataforma, compensando la deriva del giróscopo con la dinámica lenta del inclinómetro \cite{baerveldt2002low}.
El filtro complementario propuesto es el que se muestra en la figura siguiente. Donde
es el ángulo medido por el acelerómetro cuya señal esta corrompida por ruidos de alta frecuencia proveniente de las vibraciones,
es el ángulo medido por el giróscopo, afectado por la deriva y
es el ángulo estimado.
Diagrama en bloques del filtro complementario utilizado:
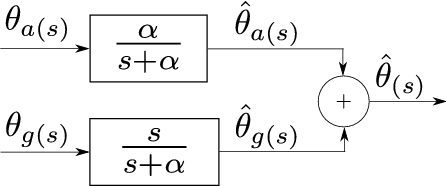
Las funciones de transferencia del filtro deben ser elegidas de acuerdo a la ecuación:
en donde
y
representan las funciones de transferencia del acelerómetro y el giróscopo respectivamente.
Suponemos que las funciones de transferencia de las sensores son iguales a 1. Esto es
.
La función de transferencia elegida para
es un filtro pasa bajos de primer orden, lo cual hace que la estimación en baja frecuencia dependa de la medición del acelerómetro.
Y la función de transferencia para
:
este filtro nos permite hacer que las componentes de alta frecuencia de la medición estimada estén dominadas por el aporte de las mediciones provenientes del giróscopo.
Como podemos ver en el diagrama en bloques del filtro, si ambas mediciones son ideales, la función de transferencia total del filtro resulta:
Y esto hace que:
Discretización de los filtros
Para la implementación de los filtros digitales en el microcontrolador se parte discretizando las funciones de transferencia de los mismos usando la transformada z y suponiendo un retenedor de orden cero a la entrada. Con esto se obtiene una expresión compacta para el filtro completo.
Si definimos:
y
, entonces:
En donde
y
representa la constante de ambos filtros.
Algoritmo del microcontrolador
El algoritmo del microcontrolador surge del paso a ecuaciones en diferencias de las funciones de transferencia de cada filtro.
Resultados de la implementación
Se ensayó el sistema utilizando el filtrado complementario verificándose una buena estimación del ángulo que resultó en la correcta estabilización y una buena respuesta dinámica.
En la figura siguiente se muestran las mediciones individuales del acelerómetro y el giróscopo; y la estimación del filtro complementario; mientras se sometió al sistema a perturbaciones forzándolo a salir de la posición de equilibrio y permitiéndole que se restituya en forma autónoma.
Como se observa en la gráfica se calibró débilmente el offset del giróscopo para permitir una deriva exagerada a fin de mostrar el rechazo del filtro.
Mediciones y estimación durante ensayo del sistema:
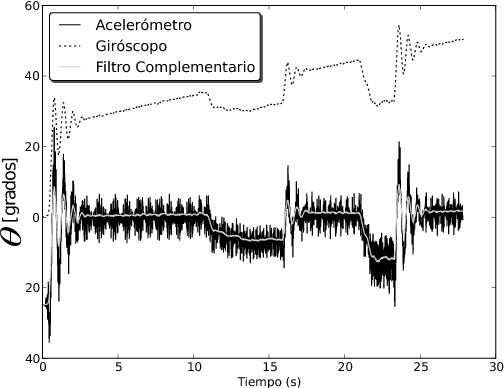
En la figura siguiente se observa la medida del ángulo estimada por el filtro contrastada contra la medición del potenciómetro durante la evolución del sistema desde un ángulo inicial de -10 grados hasta el equilibrio en cero grado. En este ensayo se utilizó la medida del filtro para la realimentación del lazo de control y se ajustaron las constantes del controlador PID. Este ajuste se realizó según los análisis de estabilidad hechos del sistema a lazo cerrado para obtener la respuesta subamortiguada que se observa, aunque hubo que realizar algunos retoques empíricos los cuales se pueden deber a que se idealizaron algunas partes del sistema y también a falta de una buena calibración de los sensores y propulsores.
Respuesta dinámica del sistema ante una perturbación:
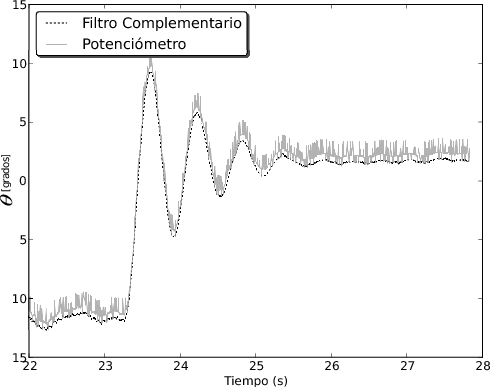
Conclusiones sobre las técnicas probadas para la estimación del ángulo
Se ensayaron tres métodos de medición de inclinación de una plataforma experimental que se comporta como el QA3 con cinco grados de libertad restringido, permitiendose rotaciones que corresponderían al cabeceo o el rolido de la aeronave. Los dos primeros métodos ensayados utilizaron acelerómetro por un lado y giróscopo por otro de manera individual. En el primer caso la influencia de las vibraciones impide el correcto funcionamiento del lazo de control, en tanto que si se filtra la señal de la medición se degrada la respuesta dinámica o incluso se llega a la inestabilidad del sistema para frecuencias de corte demasiado bajas. Por el lado del giróscopo se obtuvo mejores resultados en el comportamiento del lazo de control, no obstante esto la deriva producida por el offset del sensor hace que el error de inclinación se incremente de manera constante en el tiempo. Ninguno de los dos métodos resulta viable para el control de actitud del QA3.
Finalmente se aplicó un filtro complementario para combinar la medición de ambos sensores tomando de cada uno la parte del espectro de la señal de medición menos corrompida y atenuando la otra a fin de que la suma permita una estimación aproximada de la variable de interés.
El comportamiento dinámico del sistema realimentado con la medición estimada por el filtro resulta satisfactorio para ser aplicado al prototipo real.
Hardware de control
En este capítulo se explica el funcionamiento del hardware de control utilizado.
Placa del Microcontrolador
Una de las especificaciones pedidas por el centro para la construcción del QA3 fue el uso de la placa madre diseñada por el CIII. Esta placa madre genérica tiene la ventaja de poder ser utilizada en múltiples proyectos.
Esta plataforma contiene un microcontrolador LPC2114/24 con núcleo ARM7 y toda la electrónica asociada para realizar la programación y testeo de los sistemas diseñados. Además en el mismo centro se desarrollan un conjunto de librerías para facilitar el uso de los periféricos.
Algunas características y periféricos de este microcontrolador son:
- 16/24K RAM
- 128/256K flash
- CPU con una velocidad maxima de 60MHz
- 4 canales A/D de 10 bit
- Interfaces series UART, I2C y SPI
- Dos timmers de 32 bit
- 6 PWM
- Reloj en tiempo real
- Hasta 46 I/O de proposito general
El circuito esquemático de la placa se muestra en la siguiente imagen.
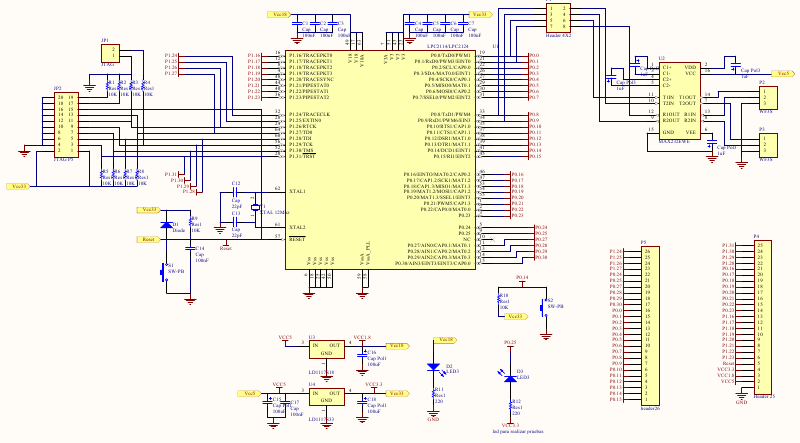
Los componentes utilizados en la placa se encuentran en el mercado local, y para su diseño se empleó exclusivamente software libre, particularmente KiCAD
Sensores
Para obtener una estimación de la posición angular del QA3 se usan 2 sensores, estos son un giroscopio de 3 ejes y una acelerómetro de 3 ejes. Luego estas 2 mediciones de fusionan a través de un filtro complementario para obtener una estimación de los ángulos. Esta fusión se explica en capítulos siguientes.
Giroscopio

El sensor utilizado para medir velocidad angular es el ITG-3200. Este sensor es un giroscopio con salida digital a través del bus
, entregando mediciones correspondiente a los 3 ejes Y, X y Z. Cada medición realizada en su correspondiente eje, es digitalizada por 3 conversores A/D que entregan la información sobre un ancho de 16 bits. Posee un filtro pasa bajos programable, un sensor de temperatura y un oscilador con 2% de precisión.
Su tensión de alimentación es muy flexible y va desde 2.1V hasta los 3.6V. Su tensión de lógica se encuentra separada y puede ir desde 1.71V hasta VDD.
Los sensores giroscópicos MEMS utilizan miden la velocidad a través del efecto Coriolis.
Estos sensores tienen la principal ventaja de ser muy inmunes a la vibración, pero tienen como principal desventaja una deriva en la salida obtenida. Esta deriva hace que si necesitamos calcular el ángulo a través de integración obtenemos un error sistemático que hace que le medición del ángulo tienda a infinito. Debido a esto se usa el acelerómetro para corregir esta deriva.
Acelerómetro
Luego de realizar distintas pruebas sobre distintos sensores de aceleración, se optó por el ADXL345. Por su excelente relación costo-beneficio. Este sensor al igual que el anterior es de tipo MEMS.

El sensor ADXL345 contiene salida digital a través del bus
o SPI, brindando una resolución de 13 bits por cada eje y hasta un rango de
. Su resolución tanto como su rango son programables y puede discernir hasta 1.0º de inclinación utilizando la configuración de máxima resolución.
Una de las principales desventajas de los acelerómetros es su alta sensibilidad a las vibraciones, lo que hace que su uso como inclinómetro nos permite solo hacer mediciones a largo plazo de la inclinación.
Circuito de montaje de los sensores
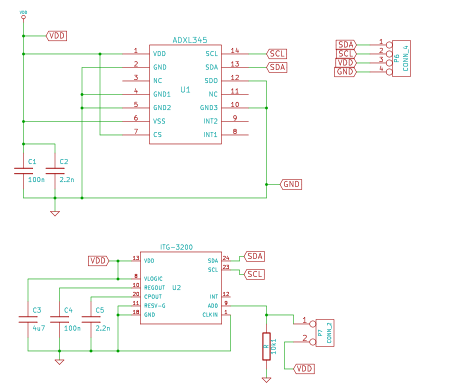
Driver de motores ESC
Los controladores de los motores (ESC, Electronic Speed Controller) permiten regular la potencia suministrada a cada motor. Para controlar la potencia de los motores utiliza una señal servo convencional: un tren de pulsos cuadrados de período T y ciclo de trabajo W variable (0 % y 100 % respectivamente).
Inicialmente se optó por diseñarlos, se propuso un esquemático compuesto por 6 MOSFETs, un microcontrolador que haga de interfaz con el exterior y que excite a los MOSFETs. Luego se procedió a la búsqueda de los componentes y encontramos un impedimento al no conseguir los MOSFETs de estas características(100A, 12V) en el mercado local. Al tener que importarlos, se comenzó con el análisis de costo-beneficio y resultó ser mas conveniente utilizar los ESC disponibles en el mercado, ya que cumplen con los requisitos necesarios para el proyecto.
Los controladores elegidos también son RCTimer de 30A. Se alimentan con una tensión que se pueda formar con celdas LiPo que en este caso se conectan en serie para lograr un voltage de 11.1V. La conexión al motor tiene tres cables (motor brushless).

Características:
- Voltage de entrada:DC 6-16.8V(2-4S Lixx)
BEC:5V 2amp
- Corriente de trabajo: 30A (Output: Continuous 30A, Burst 40A up to 10 Secs.)
- Dimensiones: 36mm (L) * 26mm (W) * 7mm (H).
- Peso: 32g.
La frecuencia de trabajo que se utilizó es de 200Hz, ya que era lo suficiente para cerrar el lazo de control.
Conexión inalámbrica
Para controlar el QA3 ya sea a través de un joystick, de una cámara o algún sensor externo, es necesario algún medio de comunicación inalámbrico. Se analizaron las opciones disponibles en el mercado y se optó por utilizar una conexión Wi-Fi(802.11). Este tipo de conexión permite conectarse directamente a otra PC, o a un router donde pueden existir muchas PCs conectadas, evitando así, hardware extra en la PC que realice el control a largo plazo.

El módulo utilizado es el WiFly GSX. Es un sistema embebido que brinda una solución completa de acceso wireless, requiriendo únicamente 4 pines de conexión (POWER, TX, RX, GND) para ser utilizado. Una vez que la configuración ha sido establecida, el módulo puede acceder automáticamente a una red WiFi y comenzar a enviar/recibir paquetes, a través de datos serie.
Desde el microcontrolador funciona de modo transparente, donde la conexión es exactamente igual a una configuración null modem sin handshaking.
El módulo WiFly GSX (RN-131C) es una completa solución embebida de ultra bajo consumo para TCP/IP. La WiFly GSX es un módulo de red wireless 802.11b/g embebido independiente. La combinación de ultra bajo consumo y la habilidad de auto despertarse, conectarse a una red wireless, enviar datos y volver al estado de dormida en menos de 100ms, le permiten a la WiFly GSX funcionar por años con 2 baterías estándar AAA. Usando solo 100 mW cuando está despierta y 10 uW cuando esta dormida, esta marcada eficiencia de potencia, hace posible una nueva clase de dispositivos con internet disponible.
El módulo WiFly GSX incorpora una radio de 2.4GHz, procesador, stack TCP/IP, reloj en tiempo real, acelerador de encriptación, manejo de potencia y interfaz con sensores analógicos. Esta solución completa esta pregrabada con software para simplificar la integración y minimizar el desarrollos de las aplicaciones. En la configuración más simple el hardware requiere solo 4 conecciones (PWR, TX, RX, GND) para crear una conexión de datos wireless. El rango de alcance puede ser de 100m, dependiendo de las condiciones del entorno.
Características
- Ultra bajo consumo, 100mWatt activa, 10uWatt modo reposo
- Tasa de transferencia con el host de hasta de 100 Mbps para SDIO, 44 Mbps para SPI y 2.7 Mbps para UART
- Salida de 1 Mbps con TCP/IP y WPA2
- Interface de hardaware UART
- 10 entradas salidas de propósito general
- 8 interfaces analógicas para sensores
- Reloj en tiempo real para despertarse y dormirse automaticamente y para medición de instantes de tiempo
- Acepta 3.3VDC regulados o 2-3VDC desde una batería
- Soporta conexión ad-hoc
- Configuración a través de las interfaces UART o wireless usando simples comandos ASCII
- Actualización del firmware a través del aire, y a través de un archivo
Autenticación WiFi segura WEP-128, WPA-PSK (TKIP), WPA2-PSK, EAP-TLS para WPA1 & WPA2 Enterprise
- Aplicaciones de red incorporadas, DHCP, UDP, DNS, ARP, ICMP
Diagrama en bloques
En la figura siguiente se muestra el diagrama en bloques interno del módulo wirelesss.
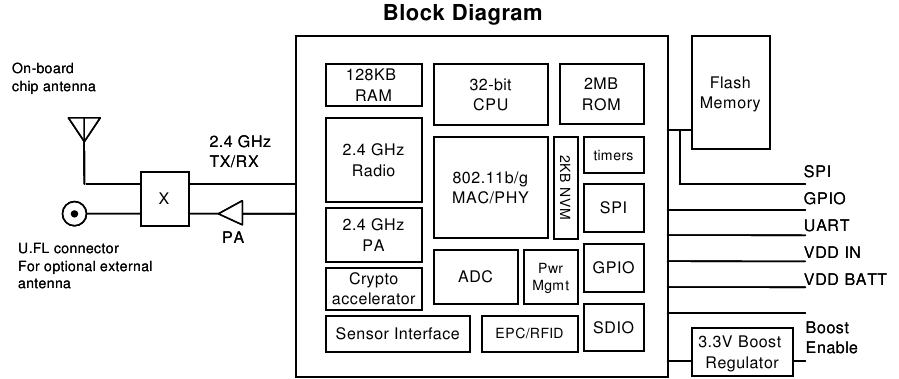
Circuito Esquemático
El circuito esquemático utilizado se muestra en la siguiente figura.
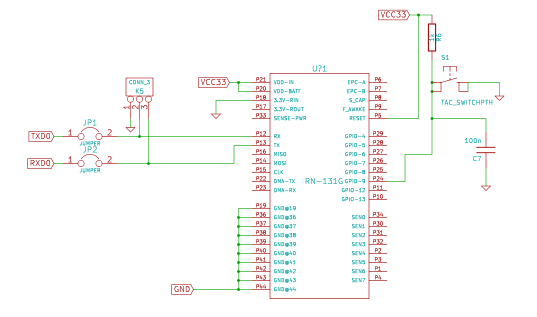
Comunicación
La comunicación entre el micro y la wifly se realiza a través de la UART, con la misma configurada a 115200 bps, sin control de flujo, con 8 bits y sin paridad.
La comunicación entre la PC y la wifly se realizó a través de wifi, utilizando el protocolo UDP. También se podría haber utilizado el protocolo TCP, pero consideramos más importante obtener una baja latencia en la comunicación.
La red wireless se configuró en el modo ad hoc. Una red ad hoc es aquella en la que no hay un nodo central, sino que todos los dispositivos están en igualdad de condiciones. Se eligió este modo porque además de ser el más sencillo para el armado de una red, es el que viene configurado por defecto en el módulo wifly.
Placa Base
Por último de construyo una placa base sobre la cual se montaron todos los componentes nombrados anteriormente. El circuito esquemático se muestra en la figura siguiente.
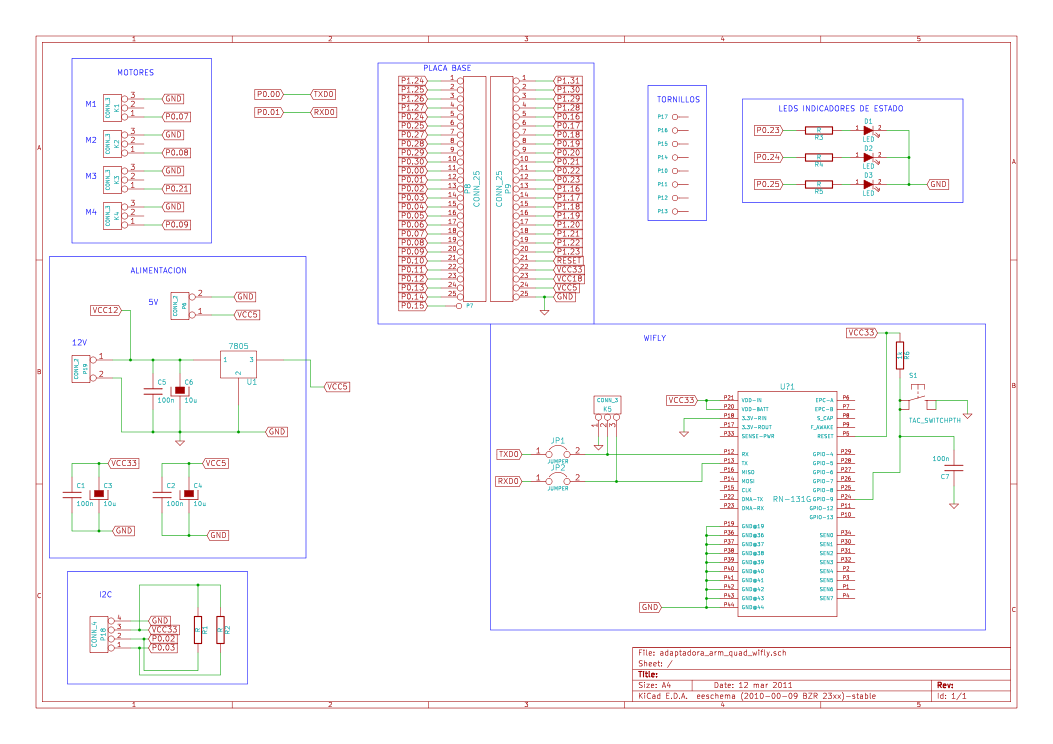
Como se puede apreciar en la misma, vemos 4 conectores para los PWM de los motores, un regulador para obtener desde la tensión de 11.1V de las baterías los 5V necesarios para la alimentación, también vemos un conector para la placa adaptadora de los sensores mems, leds indicadores y por último el módulo wireless.
Software
El software consta de dos partes totalmente desacopladas, una es el control de lazo cerrado a corto plazo el cuál controla los 3 grados de libertad (roll, pitch y yaw), y la otra es el software de la PC que establece el control de lazo cerrado a largo plazo que controla los otros 3 grados de libertad (y, x y z).
Firmware ARM
El software de control es del tipo secuencial, en lenguaje ANSI-C, haciendo uso de los periféricos y características que ofrece el uC a través de la placa multipropósito, como timers, UARTs, PWMs, detección de flancos, entre otros. El siguiente diagrama de flujo simplificado da una noción del flujo seguido por el software.
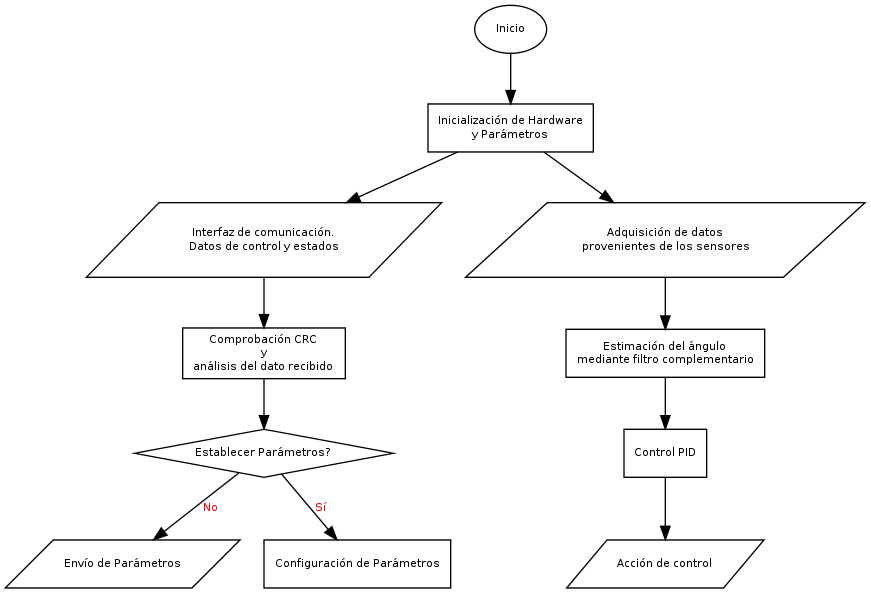
Como vemos consta de dos tareas principales, una es la interfaz con el mundo exterior. En la cuál los datos pueden ser parámetros en ese instante o establecer alguno de ellos para realizar el control del mismo.
La comunicación es realizada a través de la UART, se estableció un protocolo para intercambiar con la PC. Luego de varias fallas, se decidió implementar una comprobación de errores optando por la comprobación de redundancia cíclica(CRC). Tiene dos modos de envíos de parámetros, uno síncrono y otro asíncrono.
- El modo síncrono es desde el uC hacia la PC, cada vez que obtiene datos de los sensores son enviados inmediatamente.
- El modo asíncrono es desde la PC hacia el uC. La PC cada cierto tiempo le envía un dato solicitándole un parámetro específico, el uC envía el parámetro que tiene en buffer.
Todo el firmware para el QA3 fue desarrollado con herramientas libres. Como editor de texto no se utilizó entorno gráfico alguno, solamente el editor Vim. Como toolchain de compilación, se utilizó gcc cross-compiled para ARM. Para grabar el microcontrolador se utilizó lpc21isp y por último como herramienta de debug se utilizó insight con la interfaz JTAG.
Los 2 algoritmos fundamentales del firmware son el filtro de estimación del ángulo y el controlador PID. Las partes principales se muestran a continuación.
Código del filtro complementario
1 void filtro_complementario(void) {
2 //Cálculo de Phi
3 angulo.Phi_est = 0.9981 * (angulo.Phi_ant) + 0.005 * velocidad.Phi + 0.0019 * angulo.Phi_med;
4 angulo.Phi_ant = angulo.Phi_est;
5 angulo.Phi = angulo.Phi_est - angulo.Phi_zero;
6 //Cálculo de Theta
7 angulo.Theta_est = 0.9981 * angulo.Theta_ant + 0.005 * velocidad.Theta + 0.0019 * angulo.Theta_med;
8 angulo.Theta_ant = angulo.Theta_est;
9 angulo.Theta = angulo.Theta_est - angulo.Theta_zero;
10 }
Código del controlador PID
1 void pid_update(pid_type* pid){
2 pid->error = pid->in - pid->ref;
3 pid->proportional = pid->Kp * (pid->error - pid->error_old1);
4 pid->integral = pid->Ki * pid->error;
5 pid->derivative = pid->Kd * (pid->in - 2*pid->in_old1 + pid->in_old2);
6
7 if(pid->in >= 5 || pid->in <= -5){
8 pid->integral = 0.1 * pid->integral;
9 }
10 pid->out = pid->out_old + pid->proportional + pid->derivative + pid->integral;
11 pid->in_old2 = pid->in_old1;
12 pid->in_old1 = pid->in;
13 pid->error_old1 = pid->error;
14 pid->out_old = pid->out;
15 }
Software de control de la PC
El software de la PC está realizado en python y se comunica por medio de una conexión socket tcp a través de la placa inalámbrica. Se encarga de tomar las lecturas del joystick, procesarlas y luego enviarlas al uC. También este programa lleva una bitácora con los tiempos de vuelo y datos obtenidos en ese momento en un período de 100ms cada muestra, definiendo la actitud del robot en espacio-tiempo. Para luego ser utilizado en corrección de errores, calibración de las mediciones realizadas, ajustes del controlador, análisis de vibraciones, etc.
También permite establecer los parámetros del control, tanto como los ceros los ángulos
,
y
, como así también los valores de
,
y
de los PIDs.
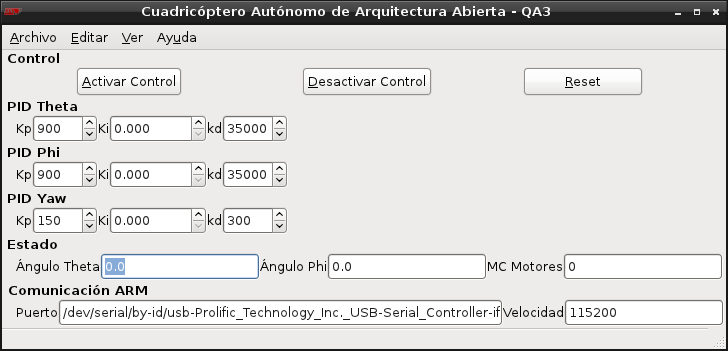
Utilidades adicionales
Se generaron herramientas que permitieron el testeo y depuración del sistema.
Por ejemplo en el momento de análisis de vibraciones, se generaron gráficos de distintos instantes de tiempo y su transformada rápida de Fourier. Permitiendo así obtener las distintas respuestas al impulso hasta lograr un valor óptimo.
También se realizo una interface entre la PC y la balanza usada para medir el empuje de los motores.
Todas estas herramientas para analizar los datos obtenidos se escribieron en lenguaje python.
Conclusiones
Se ha logrado la construcción de un robot autónomo volador con 3 grados de libertad controlados, apropiado para vuelos en interiores. Se priorizó la utilización de componentes de bajo costo, aunque la mayoría de estos no se consiguen en nuestro país.
El robot construido cuenta con una estructura robusta y con una carcaza de protección, la cual previene de roturas de las hélices y accidentes que puedan dañar al usuario.
La carga útil del prototipo es de aproximadamente 1kg, la cual nos permite agregar en un futuro una unidad de procesamiento con mayores capacidades y cámaras para lograr a través de algoritmos de procesamiento de imágenes una estabilización en los 6 grados de libertad y una mejora en la respuesta global del sistema.
Una de las ventajas del prototipo realizado es su arquitectura abierta, la cual en este caso abarca el uso de herramientas informáticas libres y gratuitas para su desarrollo, la disponibilidad de los planos mecánicos y circuitos eléctricos a través de la página del CIII y también de la documentación asociada al proyecto.
También se ha realizado un estudio exhaustivo del modelo dinámico del QA3, el cual puede permitir en un futuro el diseño de algún otro controlador ya sea lineal o no lineal, el cual puede tener en cuenta algunas de las variables despreciadas en el controlador actual.
Se ha logrado la construcción de una Unidad de Medición Inercial ( IMU ) de reducido tamaño, la cual integra 3 sensores ( acelerómetro, giróscopo y magnétometro ) de bajo costo; esta IMU no solo se puede utilizar para este robot, sino que puede ser usada para desarrollos futuros del propio centro de investigación o como punto de partida de otras tesis o trabajos.
El desarrollo de este proyecto también ha generado la presentación y aprobación de un artículo en el Simposio Argentino de Sistemas Embebidos, cumpliendo también con uno de los objetivos personales de los integrantes del grupo de trabajo y también con los objetivos del CIII.
Otra de las ventajas que queremos destacar del diseño es la utilización de software libre en todas las etapas del desarrollo.
Análisis de Costos
Se pudo lograr la construcción de un dispositivo de bajo costo y altas prestaciones en comparación con otros disponibles comercialmente. Aunque la principal ventaja del prototipo diseñado es su arquitectura abierta, la cual le permite a cualquier persona obtener los planos mecánicos y electrónicos, el código del firmware del microcontrolador y el de la PC sin costo alguno. También realizar cambios sobre los mismos para poder adaptar el prototipo al uso particular. Esta arquitectura también es la que mejor se adapta al ámbito de la investigación, debido a que en este entorno se necesita tener control sobre todos los parámetros del sistema en el cual se hacen pruebas y para esto es necesario que los circuitos estén disponibles, que también el firmware este disponible y que las herramientas informáticas necesarias para desarrollarlo no tengas altos costos.
A continuación se hace un detalle del costo del prototipo.
Costo detallado del Prototipo
Componente |
Cantidad |
Costo Unitario |
Sub Total |
Estructura |
1 |
60 |
60 |
Motores |
4 |
60 |
240 |
ESC |
4 |
40 |
160 |
Hélices |
4 |
5 |
20 |
Baterías |
2 |
240 |
480 |
Cargador |
1 |
300 |
300 |
Placa Madre |
1 |
200 |
200 |
Sensores |
1 |
160 |
160 |
Wireless |
1 |
200 |
200 |
Total |
1820 |
||
Desarrollos a Futuro
Como el prototipo diseñado surge para ser usado en tareas de investigación, se planea continuar con el desarrollo del mismo agregando nuevas funcionalidades.
Se planea agregar un sistema de cámaras para poder obtener una referencia absoluta de posición y luego con estos datos obtener un control sobre los 6 grados de libertad, lo cual nos permitiría obtener un dispositivo realmente autónomo. El tratamiento de las imágenes obtenidas a través de la cámara necesita un alto requerimiento computacional por lo tanto se agregará una SBC (single board computer) desarrollada en el CIII para poder realizar este tratamiento matemático.
También se completará la IMU con un magnetómetro para obtener una referencia absoluta para el ángulo de yaw y la construcción de un altímetro para obtener una referencia de posición en el eje z.
Otra de las mejoras que se debe realizar en el prototipo es la construcción de una estructura más liviana, con el mismo material o con otros materiales usados en aeromodelismo como puede ser fibra de carbono.

